Von Mise stress higher than Max Principal Stress?

[jmarroquin]

Hi all, I am currently working on an analysis for a mechanical I designed, but when I run the design study, it gives me results showing the von mise is higher than the max principal. How can that be? I feel I have constrained it properly, but just wondering. Has anyone had this issue?

This thread is inactive and closed by the PTC Community Management Team. If you would like to provide a reply and re-open this thread, please notify the moderator and reference the thread. You may also use "Start a topic" button to ask a new question. Please be sure to include what version of the PTC product you are using so another community member knowledgeable about your version may be able to assist.

[346gnu]

Hi,

You need good constraints to get good answers but the relationship between Von Mises and  Principal stresses has nothing to do with the constraints whether the constraints be right or wrong.

It is possible to have biaxial Principal stresses greater than uniaxial yield without yielding (according to Von Mises).

It is possible to have zero Von Mises stress when the principal stresses are equal (hydrostatic).

I can't see how it is possible for Von Mises ever to be greater than the Max Principal.

This is maths. Has someone got a simple proof or the required logic?

More practically, Use measures to get the values of principal stresses and Von Mises stress at a point of interest.

Work out the Von Mises by hand.

[mlindqvist]

If, for example, you have a Square block with uniaxial tensile stress, then von Mises = max principal. If you add a compressive stress from the sides, then the von Mises will be greater than the max principal, which stays the same. Look at the formula for von Mises. If I remember correctly, you will see something like Svm=0.5*sqrt( (S1-S2)^2+(S2-S3)^2+(S3-S1)^2), So you see that if S2, S3 are negative(i.e. comressive) then the term (S1-S2) will be greater than S1.

Sxx, Syy, S1, S2 etc.  are directional quantities, that can be either positive(tensile) or negative(comressive).

The von Mises (or Tresca) stress is a scalar number, always positive, and has no direction. Like "temperature". It tells you if you are close to, or above material yielding. If your calculated Svm is greater than the yield limit, obtained in a uniaxial test, then the material will yield. The purpose of the vonMises/Tresca yield criteria, is to determine if there is yield in a multiaxial stress state. If you pull the material in one direction and simultaneously compresses it in the perpendicular direction, then it is easier to obtain plastic deformation, compared to if only pull the material. The von Mises takes this into acount.

[346gnu]

Yes Von Mises is unsigned; always positive and no direction.

You're right. (but the 0.5 is inside the sqrt ).

A simpler example would be where all principal stresses are compressive (negative).

Von Mises stress is positive; therefore greater. QED

Svm=sqrt(0.5*[ (S1-S2)^2+(S2-S3)^2+(S3-S1)^2])

if s1=s2=s3 (regardless of sign) Svm=0

if s1=1, s2=-1, s3=-1 (your example) then Svm=2

if we state that 1=yield and set s1=1.15, s2=0.5, s3=0 then Svm=1 and s1>uniaxial limit without failing

[unickque]

https://en.wikipedia.org/wiki/Von_Mises_yield_criterion

[rubenvillarreal]

Excellent question,

The answer is no.

Let us review the Von Mises Equation:

This equation defines the yield surface as a circular cylinder (See Figure) whose yield curve, or intersection with the deviatoric plane, is a circle with radius 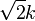, or 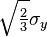. This implies that the yield condition is independent of hydrostatic stresses.

Basically, all possible combinations of principal stresses (compression and tension) will form an ellipse. Each point of that ellipse is called "The Von Mises Stress" for each particular combination of principal stresses. With only two principal stresses the ellipse is as follow:

So, notice that no matter the combination of stresses, the most critical situation that you can find is that a principal stress has the same exact value than the von mises stress 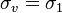which means that you are in the edge of the ellipse, and your factor of safety according to Von Mises theory is exactly 1.

Of course, in real experiments a principal stress can be a little higher than the Von Mises stress, take a look at this graph and notice the points of failure outside the ellipse.

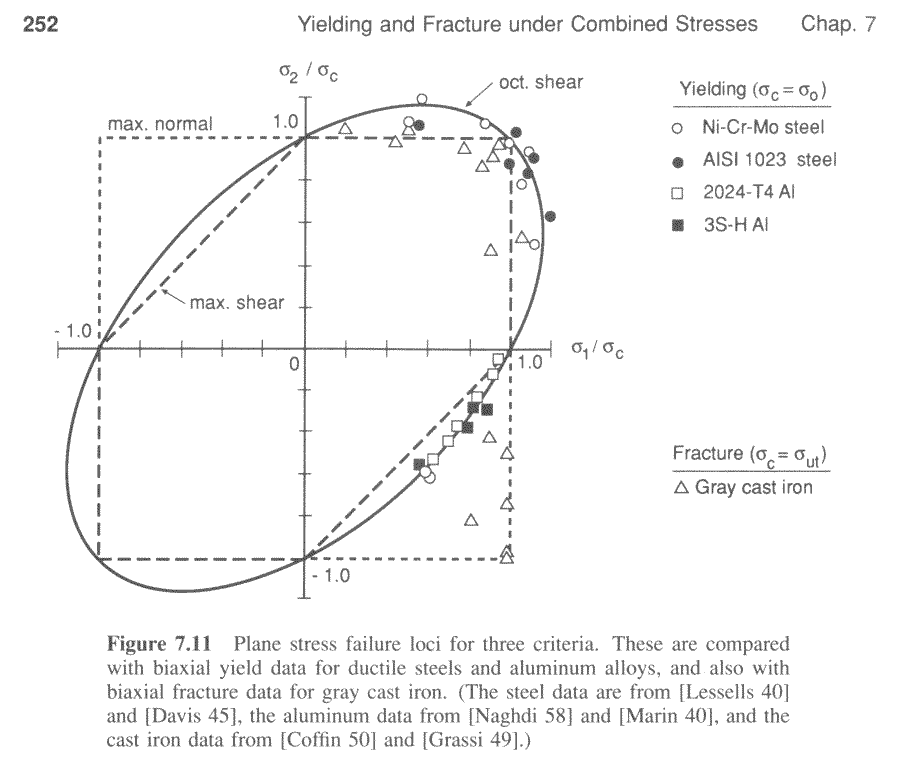
Now, the problem that you have. Remember that FEM it is only an approach to solve a quite complicate ordinary differential equation. You will not ever get the exact result. Also, it is your responsibility to check if the code of the engine solver is working right. Notice this about Creo Simulate:

"If the interpolating polynomial for the spatial variation of the displacement field is linear within an element, then the strains and stress within are constant. Furthermore, the stresses are only continuous (smooth) within an element. At the border of the neighbor element, stresses may become discontinuous (jump). This difference is usually smoothed away in the post-processor by different averaging techniques. This difference can also be used for error estimation and convergence improvement during the solution process. Simulate uses superconverged stresses for this purpose, as described in a later module."

So, check the elements, check the convergence, and check the simulation again, maybe what you get is a little difference caused by number noise. Otherwise, you should contact PTC directly to inform about this.

The other thing that may be happening, is that your piece is in failure, so check that also, hahaha.

Have a nice day!

[unickque]

Ruben Alejandro Villarreal Barrios wrote:

Excellent question,

The answer is no.

What was the question?

(You make it sound like "No, Von Mises stress can never be higher than Max Principal stress" which is incorrect, as Charles Simpson pointed out in his example)

[rubenvillarreal]

Oh but Charles Simpson point was exactly my point,

Quoting him "It is possible to have zero Von Mises stress when the principal stresses are equal (hydrostatic).

I can't see how it is possible for Von Mises ever to be greater than the Max Principal."

You can get higher principal stresses with the hydrostatic principle, yes. BUT! That's another question.

I asked two different teachers about if hydrostatic tension could cause failure.

The first one told me "No, you could through a screw into the ocean and hydrostatic pressures will not cause failures on it no matter the depth"

The second told me "If you go directly into a black hole where hydrostatic tension are infinite, something will happen to you"

The second, also told me that the Von Mises cylinder is not infinite, there are some theories that limit its region. I believe what the second teacher told me.

In the example below that answer, quoting it "If, for example, you have a Square block with uniaxial tensile stress, then von Mises = max principal. If you add a compressive stress from the sides, then the von Mises will be greater than the max principal, which stays the same. Look at the formula for von Mises."

Is wrong, adding another stress (either in tension or compression) will change automatically the value of the Von Mises Stress.

You understood my point. "No, Von Mises stress can never be higher than Max Principal stress". And I understand your point, if all stresses remains negative, YES, Von Mises (because of the sign) will be greater. But remember, we are talking here about absolute values. Thanks to you I can correct this.

"No, Von Mises Stress absolute value can never be higher than Max Principal stress absolute value"

However I forgot the most important thing here, notice in the last diagram that most of the failures occur INSIDE the ellipse. So the question is, it is your safety factor enough? Should you use Treska instead?

[unickque]

I was referring to this bit:

Svm=sqrt(0.5*[ (S1-S2)^2+(S2-S3)^2+(S3-S1)^2])

if s1=s2=s3 (regardless of sign) Svm=0

if s1=1, s2=-1, s3=-1 (your example) then Svm=2

[unickque]

Ruben, please run attached model, check the results for von Mises stress and Max Principal stress, and explain how the results fit in your theory?

[unickque]

Yes, exactly. According to our friend Ruben Alejandro Villarreal Barrios this should not be possible. Unless I misunderstand what he is saying?

[rubenvillarreal]

THIS ANSWER HAS CRITICAL MISTAKES, REFER TO THE BOTTOM OF THIS POST, VON MISES STRESS CAN BE HIGHER THAN PRINCIPAL STRESSES.

[rubenvillarreal]

THIS ANSWER HAS CRITICAL MISTAKES, REFER TO THE BOTTOM OF THIS POST, VON MISES STRESS CAN BE HIGHER THAN PRINCIPAL STRESSES.

[DeanLong]

[unickque]

Oh come on now Dean, this is just some 2nd order equations. It's not like we're trying to solve the Reynolds equation?

[rubenvillarreal]

We do not did that, because Creo does not have the Computational Fluid Dynamics tool. Otherwise...

What a terrible disadvantage of this software isn't?

[rubenvillarreal]

Ups?

Yes, I was totally wrong about this. Von Mises stress can be QUITE HIGHER than principal stresses.

Why?

Principal stresses are a three dimensional representation of the stress state of a point, what Von Mises stress equation does is create an uni-axial equivalent stress based on these principal stresses. That "equivalent stress" can be higher than the principal stresses because you are transforming a 3 dimensional stress state into an UNIAXIAL EQUIVALENT stress state that you will use later to compare it with the yield stress and find the safety factor. This equivalent uniaxial stress has no physical components, and obviously has no direction. In your real part, you can't see it and in certain way, it doesn't exist.

I was wrong because I though that this "equivalent stress" was the result of an average stress of these principal stresses, which in such case can't be higher, but this is totally a misunderstanding about Von Mises stress theory and it's totally my fault. Patrick Asselman‌

Sorry for my mistake, I will edit my previous answer. Denis Jaunin‌

Now, I have questions,

Let's say that you graph the ellipse formed by the Von Mises stress equation. Can you graphically find the Von Mises Stress parameter? For example, when you graph a circle the equation is as follows: r^2= x^2 + y^2 and you know that r is the radius of the circle. The Von Mises stress equation for plane stresses forms an ellipse, but as with the circle, what does it mean the left side of the equation (Svm)? Is the major axis? The minor axis? Where is it?

And now we have just created this important issue:

Let us remember that Von Mises Stress theory is based on the deviatoric component of the stress state, so, according to Von Mises a piece will fail only if a deviatoric component exist, but what about hydrostatic stresses? I've been reading about this, and there is few information about it.

Norton (Strength of Materials Book) Says that rocks under the sea support such enormous pressure without fail (hydrostatic stresses), and when the same rock is tested under a uniaxial stress, it fails at lower values. So, what's happening here? How can you design something and predict failure for hydrostatic loads?

I know that there are low probabilities to design a piece that will support only hydrostatic pressure. But what about if that happens? You certainly cannot apply Von Mises stress theory in this case. It has no deviatoric component so it will not predict anything! What you should do in this case?

More important than this, what happens when principal stress has the same values? That's an hydrostatic case. And there are more probabilities to find this in real life.

And even more important than everything. Lets say that you have these principal stresses:

S1= 70

S2= 69.9

S3 = 70.1

It is quite similar to the hydrostatic case. And as we did with that case, we certainly cannot apply the von mises stress theory in this case.

Now you have the following situation:

S1= 70

S2= 69.8

S3= 70.2

As we did before, the deviatoric component is so tiny, that obviously Von Mises theory cannot be valid. Which lead us to this final question:

What do you use to decide that the deviatoric component is higher enough so Von Mises stress theory can be valid?

[unickque]

Ruben Alejandro Villarreal Barrios wrote:

Let's say that you graph the ellipse formed by the Von Mises stress equation. Can you graphically find the Von Mises Stress parameter? For example, when you graph a circle the equation is as follows: r^2= x^2 + y^2 and you know that r is the radius of the circle. The Von Mises stress equation for plane stresses forms an ellipse, but as with the circle, what does it mean the left side of the equation (Svm)? Is the major axis? The minor axis? Where is it?

You have given a very nice 3D-representation of the von Mises yield surface in 3D in your earlier posts. So that is sort of what it looks like. But of course for each point in your construction you can only draw one point in the x,y,z-stress-space. (Same thing with the circle: you will only find one R on your circle for a certain X,Y value).

And now we have just created this important issue:

Let us remember that Von Mises Stress theory is based on the deviatoric component of the stress state, so, according to Von Mises a piece will fail only if a deviatoric component exist, but what about hydrostatic stresses? I've been reading about this, and there is few information about it.

Norton (Strength of Materials Book) Says that rocks under the sea support such enormous pressure without fail (hydrostatic stresses), and when the same rock is tested under a uniaxial stress, it fails at lower values. So, what's happening here? How can you design something and predict failure for hydrostatic loads?

I know that there are low probabilities to design a piece that will support only hydrostatic pressure. But what about if that happens? You certainly cannot apply Von Mises stress theory in this case. It has no deviatoric component so it will not predict anything! What you should do in this case?

More important than this, what happens when principal stress has the same values? That's an hydrostatic case. And there are more probabilities to find this in real life.

And even more important than everything. Lets say that you have these principal stresses:

S1= 70

S2= 69.9

S3 = 70.1

It is quite similar to the hydrostatic case. And as we did with that case, we certainly cannot apply the von mises stress theory in this case.

Now you have the following situation:

S1= 70

S2= 69.8

S3= 70.2

As we did before, the deviatoric component is so tiny, that obviously Von Mises theory cannot be valid. Which lead us to this final question:

What do you use to decide that the deviatoric component is higher enough so Von Mises stress theory can be valid?

That is the whole point of Tresca and Von Mises: hydrostatic stress is irrelevant, it is only the deviatoric stress that causes yielding of the material.

If you apply a very high hydrostatic pressure on your material, maybe it will change phase and turn into another material (like carbon turning into diamond). Maybe the material will actually yield, but since it cannot 'escape', it will not deform.

But as you say, in practice this is not relevant, because high hydrostatic stresses are unlikely to occur.

If the deviatoric stress gets large enough, you will once again get yielding. Think of a forging process: the material will yield at places where the material has an escape (i.e. one of the principal stress components is small), not so much where it is only compressed hydrostatic.