1-Visitor

Solved

drawing spiral

Forum|Forum|9 years ago
June 7, 2016
5 replies
15107 views

Hi how can I draw these spiral using Relations and Pattern features?

This thread is inactive and closed by the PTC Community Management Team. If you would like to provide a reply and re-open this thread, please notify the moderator and reference the thread. You may also use "Start a topic" button to ask a new question. Please be sure to include what version of the PTC product you are using so another community member knowledgeable about your version may be able to assist.

General

Best answer by psobejko

One way is to do a dimension-based pattern a sketch which contains 2 tangent arcs:

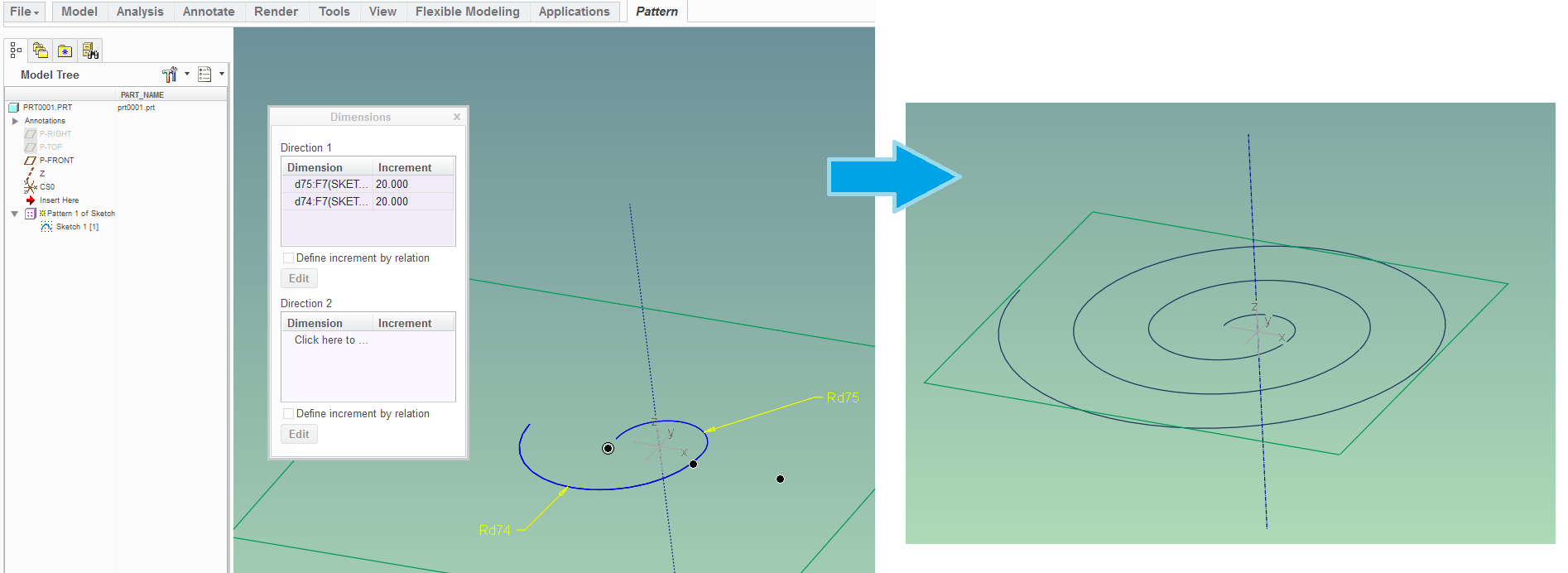
Rd75 = 10

Rd74 = 20

Both radii in the sketch are incremented in the pattern definition; so the next instance's smaller arc has the radius as the previous instance's larger arc...

I just sketched this example quickly and it worked out; but I don't know off the top of my head the formula for the increments that achieves the continuous spiral.

S

ssaiedahmad

Author

1-Visitor

thank you but how can I draw it using arc and pattern ?

P

psobejko

Answer

1-Visitor

One way is to do a dimension-based pattern a sketch which contains 2 tangent arcs:

Rd75 = 10

Rd74 = 20

Both radii in the sketch are incremented in the pattern definition; so the next instance's smaller arc has the radius as the previous instance's larger arc...

I just sketched this example quickly and it worked out; but I don't know off the top of my head the formula for the increments that achieves the continuous spiral.

S

ssaiedahmad

Author

1-Visitor

thank you Screenshot (98).png

S

ssaiedahmad

Author

1-Visitor

There is a small problem

Screenshot (99).png

K

Kevin

1-Visitor

Part of the problem is a spiral is not defined simply as two circular patterned and incremented as you have done they are specified by equations as Steve shows. You might get close with what you are doing but it's not a true spiral.

T

TrainStopper

12-Amethyst

To make a spiral that behaves according to the original post's attached picture, I would create a datum curve by equation with cylindrical coordinates.

Input IR (Inner radius), N (Number of Turns), PITCH (Pitch)

Setup the equation like this:

/* r =IR + t * (N * PITCH) , IR = Starting Radius, N = Number of Turns, t [0-1], (N*PITCH) = OR - IR, OR = Outer Radius

r = IR + t * (N * PITCH)

/* theta = t * N * 360 , theta = angle, t [0-1], N = Number of Turns, 360 = full circle

theta = t * N * 360

/* z = height , 0 = flat, t * cos(r) = helical spiral thingy

z = 0