- Community
- Creo+ and Creo Parametric
- Analysis
- Re: Fishing rod time analysis
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Fishing rod time analysis
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fishing rod time analysis
Inspired from an example viewed on a site, I've decided to try a TIME Analysis of a fishing rod during the launch.
The rod shall rotate 90deg by starting from 0 velocity and must stop at 0 velocity in 0.5sec.
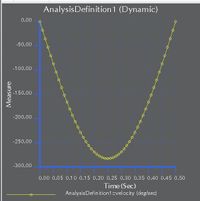
So I modeled simply the fishing rod and I done a mechanism to obtaion the curves of acceleration and torque.
The rod's material is nylon, but it could be any other one that I don't care.
Now I'm trying to do the TIME analysis in two different manners: with the base excitation (with the acceleration results) and with the load (with the torque net load results).
Apart some inaccuracies in the analysis with the load that I think they are due to the load concentration, what I've firstly seen is that the fishing rod rotation is not 90 degrees...
Could you help me?
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This was a great question!
You are correct in thinking dynamic analysis is required, however Dynamic Time uses small displacement theory. The overall motion of 90 degrees far exceeds small displacement. The relative-to-supports flex of the rod also will exceed small displacement unless the rod is very stiff. So, because of small displacement theory the tip of the rod moves in a nearly pure Y direction, which is only valid for small movements. Also, the damping removes energy so the input moment needed will be more than what the rigid body mechanism finds.
You could try putting the analysis closer to the small displacement theory by limiting the input rotation to a few degrees and stiffening the rod (maybe E large like 1000 GPa) and/or slowing the accelerations (longer time) and setting damping as 0. At some point the rigid body mechanism result should be nearly replicated by FEA, and then you can experiment from there. Plotting output relative to supports might help get things into larger rotations by removing the input rotation from the flex.
Ultimately, I think you would need a better dynamic non-linear solver than Creo provides.
-Regards
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This was a great question!
You are correct in thinking dynamic analysis is required, however Dynamic Time uses small displacement theory. The overall motion of 90 degrees far exceeds small displacement. The relative-to-supports flex of the rod also will exceed small displacement unless the rod is very stiff. So, because of small displacement theory the tip of the rod moves in a nearly pure Y direction, which is only valid for small movements. Also, the damping removes energy so the input moment needed will be more than what the rigid body mechanism finds.
You could try putting the analysis closer to the small displacement theory by limiting the input rotation to a few degrees and stiffening the rod (maybe E large like 1000 GPa) and/or slowing the accelerations (longer time) and setting damping as 0. At some point the rigid body mechanism result should be nearly replicated by FEA, and then you can experiment from there. Plotting output relative to supports might help get things into larger rotations by removing the input rotation from the flex.
Ultimately, I think you would need a better dynamic non-linear solver than Creo provides.
-Regards