Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Community
- Creo (Previous to May 2018)
- Creo Modeling Questions
- Re: worm wheel
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
worm wheel
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
worm wheel
hello everyone,
i hv made many reduction systems and never consider to show inovlute profile to worm gears/ spur gears cause i didnt wanted to give extra time to make those patterns and it may also decrease mobilty of model.. now i wish to know how to do it? if anyone knows how to make a perfect involute profile for worm wheel to match worm's thread plz post here i'm also looking for bevel....
Thanx and Regards
Dalbeer Singh Sohal
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
WOW![]() no reply
no reply
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It sounds extremely difficult.
I've modelled true involute spur gears, using an equation curve, but I haven't yet found a way to model an true helical gear, let alone a concave worm wheel.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
Check the following link
http://www.ptc.com/company/news/inprint/articles/1999_04_84.htm
I have tried to to make a rough model(without proper dimensions)
I dont have a proper dimension of gears
If you wish I can upload the model(for reference)
Regards
K.Mahanta
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
I tried to make another one
(Without proper dimensions)
I think you will like this
Regards
K.Mahanta
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
plz upload file ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
This is a worm wheel for your reference
(This does not contain actual gear data)
Regards
K.Mahanta
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
This is the origianl gear from the link (with some assumed dim)I have provided you earlier
(You can check this for your reference also)
Regards
K.Mahanta
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
didnt find the way to make exact inovlute profile ![]() ...
...
so i made this to make settlement of differences by mutual concessions.... lol
in short compermise
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not a gear designer, but aren't worm teeth straight sided?
Nice animation, by the way.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Similar to spur gear except teeth are “concaved in”.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard, to my knowledge both the worm and ring gear need to have an involute toothform or you wouldn't even be able to assemble them. And, from what I see, there is no helical lead on Dalbeers ring gear, and there should be.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
der is a helical lead but no ivolute toothform ![]()
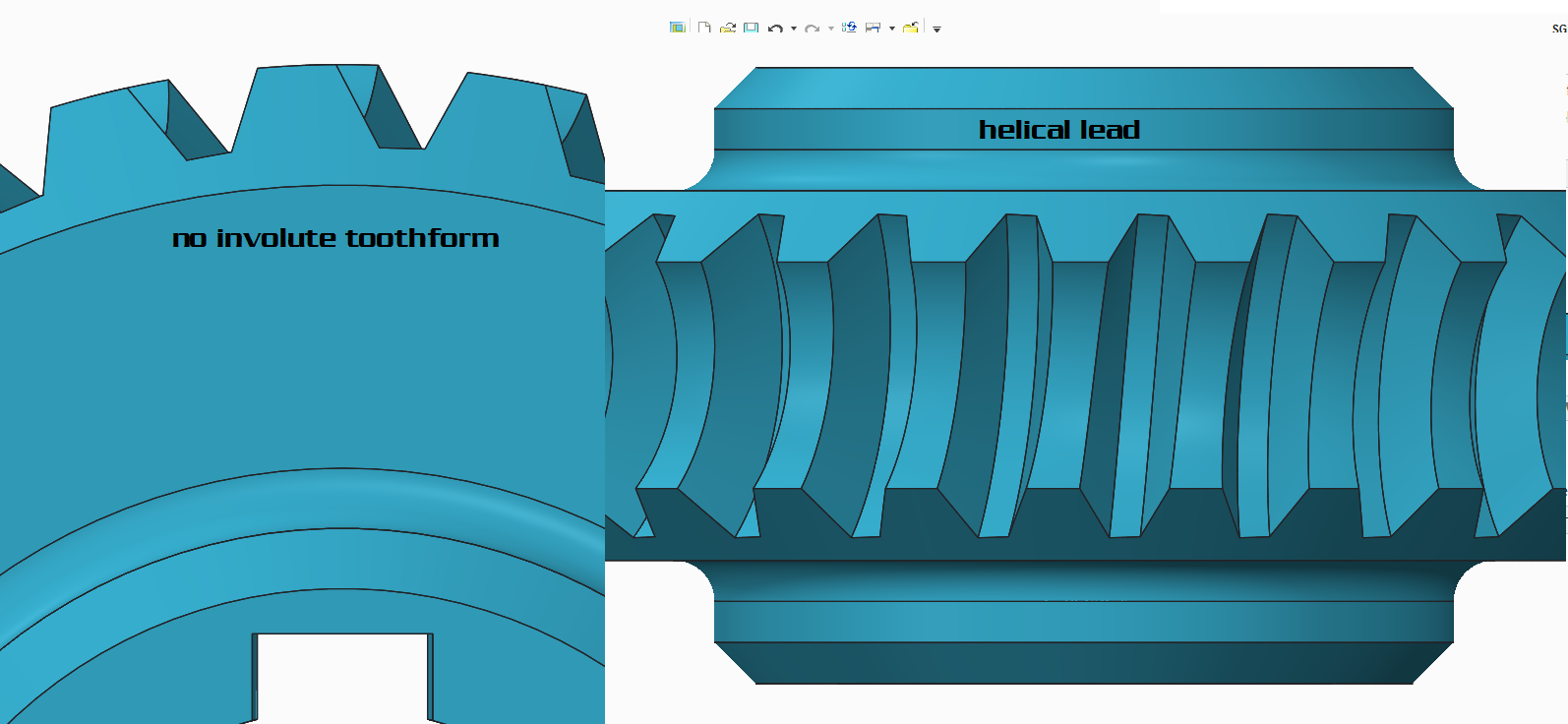
i couldnt find out the way to make a perfect involute.. still trying
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I believe Richard is correct - the worm is effectively a hob or 'rack', so is straight-sided (although helical).
The worm wheel is involute, concave and helical...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I disagree. I think every gear of any sort, to avoid point loading on the tip of the tooth and excessive wear on both gears, need to have an involute tooth form.
I'm going to research this when I have time. Any takers on that bet? ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What diameter is the base circle of the worm (or of a rack)? ![]()

