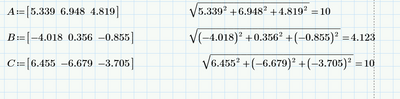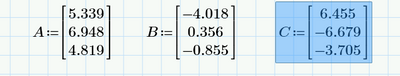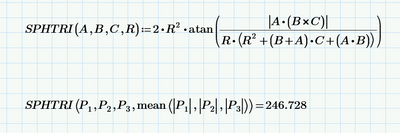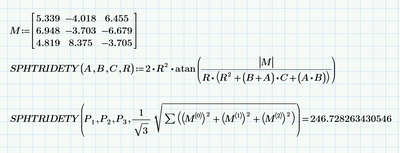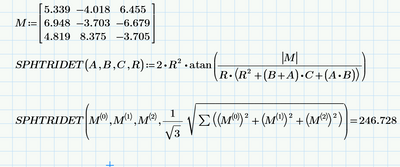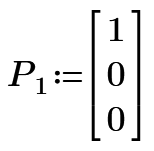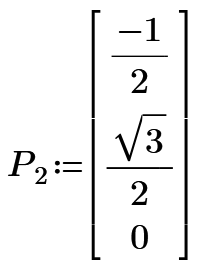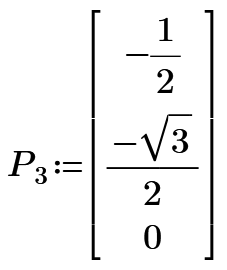Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Community
- Mathcad
- Mathcad Tips
- Mathcad Community Challenge July 2022 - Area of a ...
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Notify Moderator
Mathcad Community Challenge July 2022 - Area of a Spherical Triangle
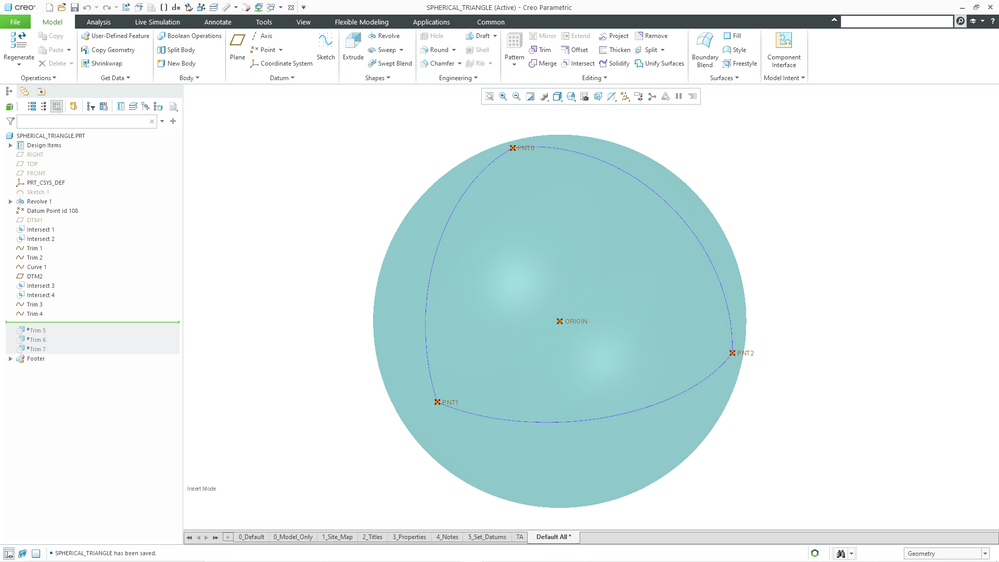
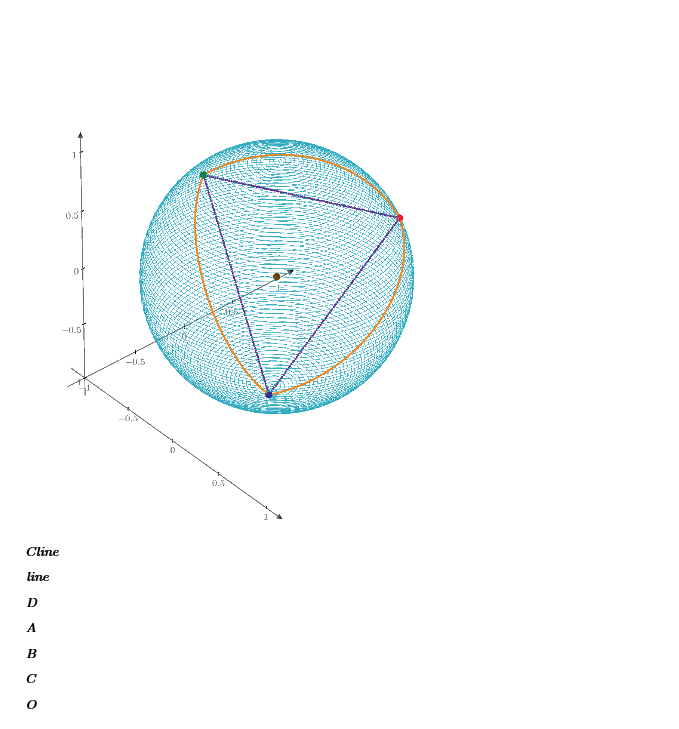
This month's challenge is another geometry-based challenge - but it's non-Euclidean geometry. Given the following three points on a circle of radius 10 units, calculate the area of the spherical triangle:
(5.339, 6.948, 4.819)
(-4.018, -3.703, 8.375)
(6.455, -6.679, -3.705)
(Note that the point coordinates are rounded to three decimal places.)
Optional:
- Can you write a program or function that calculates the area for any three points on the surface?
- Is there a symbolic evaluation for three generic points (a,b,c), (d,e,f), and (g,h,k)?
Here is a 3D model in Creo 9 of the sphere and points:
Find the Mathcad Community Challenge Guidelines here!
Edit: the coordinates of the second point were incorrect. Wildly incorrect. I have no idea how I wrote down the wrong numbers.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Are the numbers correct? I thought that the length of the vector for all three should be 10??
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Hi,
Thought I would get the ball rolling.
The coordinates supplied for three points on the sphere are correct the origin of the sphere is not at 0,0,0.
Enclosed is my solution and 3D model checking of the procedure to calculate the area.
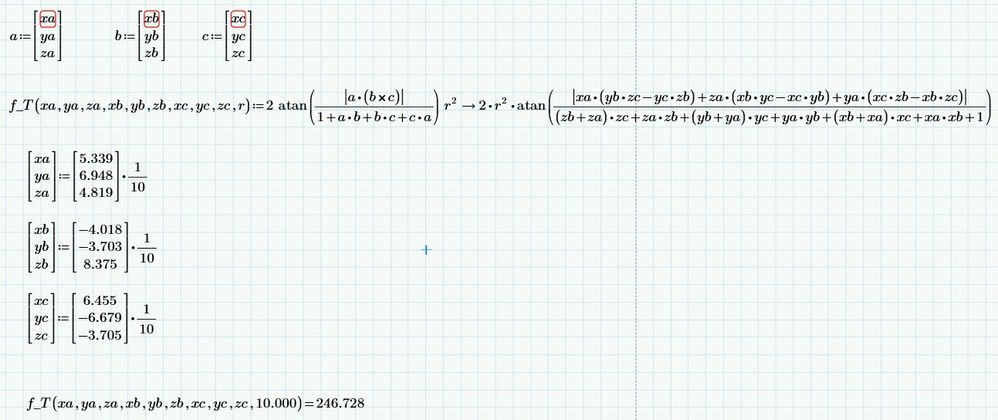
Fulfilled the first option with a program that solves for area given three points on the sphere and a radius.
Used the program in some test cases.
Cheers
Terry
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Hi,
The second optional part of the challenge was to get the spherical triangular area in terms of a,b,c,d,e,f,g,h,k being the nine xyz coordinates of the three definition points.
Here it is using an alternative to Girard's Theorem called L'Huilier's Theorem that is easier to apply.
It is a long definition so needs to be seen in draft mode.
Cheers
Terry
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
You are correct. The second point should be (-4.018, -3.703, 8.375). I have no idea why I had written down the y- and z- values so far off.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
As people realized, I wrote down the values for the second point incorrectly. The sphere has a radius of 10 and is centered at the origin. The original post has been edited to contain the correct coordinates. Thanks for catching my mistake.
For verification, I have attached the original model that I used to construct the problem. I believe I created in Creo 9.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
As pointed out by Terry - still works with the original data but the center is as follows:
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
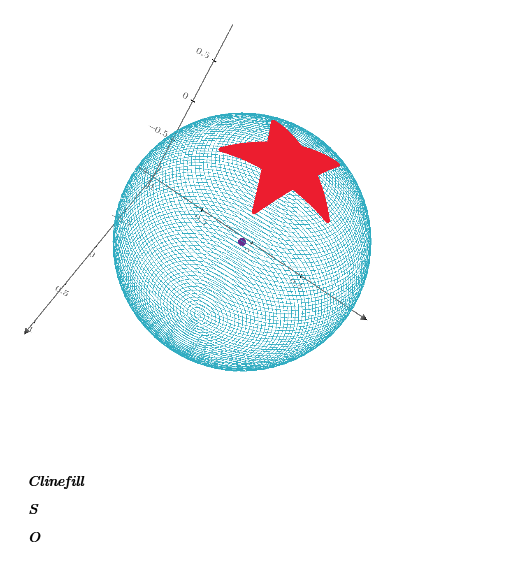
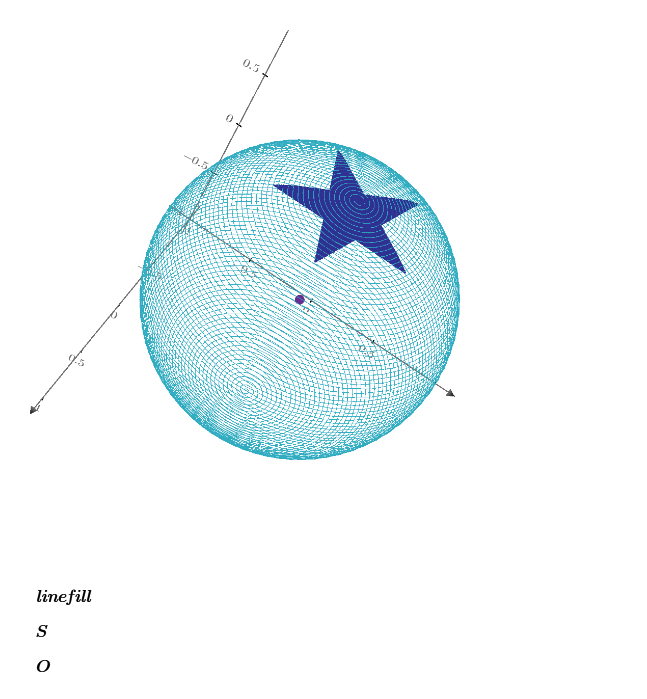
r=0.5 Blue flat star has 0.28065 and Red sphere star has 0.29736 of area.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
To myself:
or maybe this looks better?
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
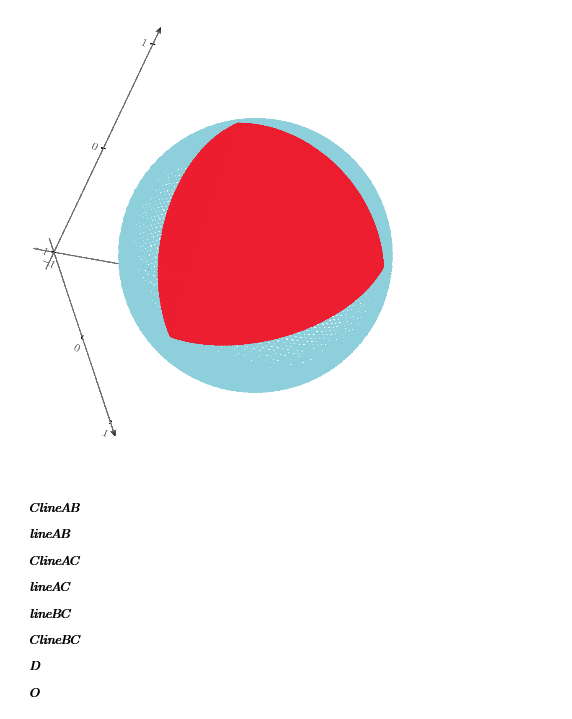
Hi ttokoro,
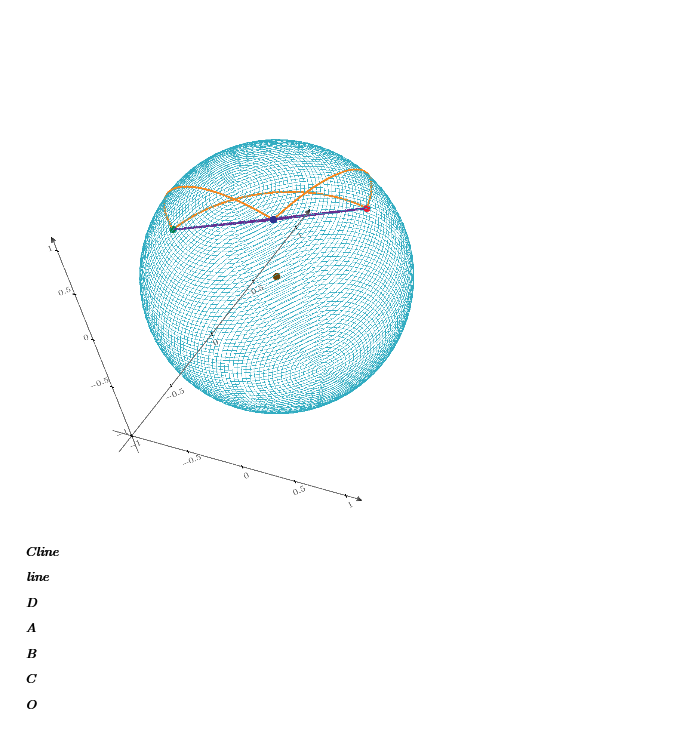
Could you upload the worksheet that generates the 3D image of the sphere and spherical triangle.
I would like to know how you have drawn the orange great circle segments please?
Cheers
Terry
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Hi ttokoro
No need I got it.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
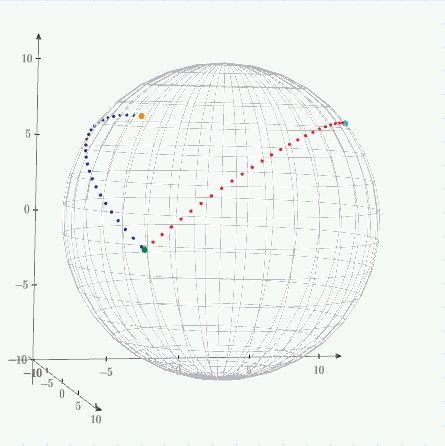
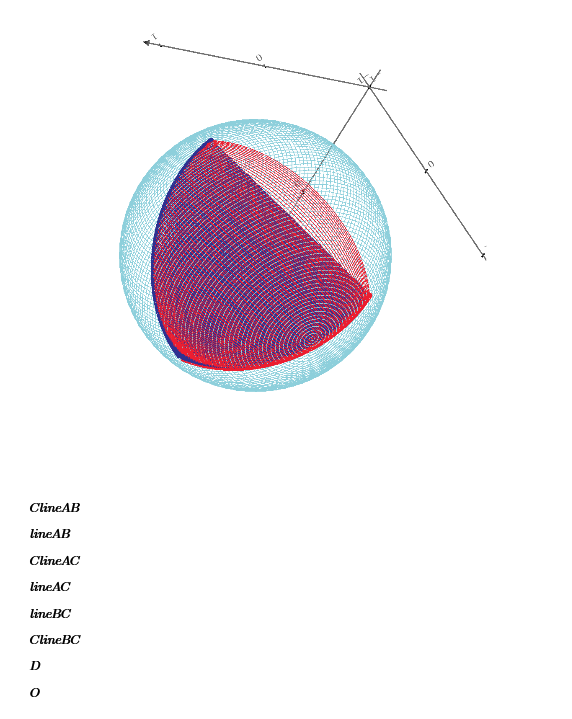
Fill the triangle on the sphere requires more Mathcad power to plot all points in red.
By the way I made this 3D plot both by Mathcad Prime8 and Maple2022, both show ABC rotation is counterclockwise and original 3D model has clockwise ABC rotation.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
or
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Quick reminder to everyone that July (and this challenge) ends soon!
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
It should be 2*Pi. Terry's sheet shows 2*Pi.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Excellent. But with the lack of comments it looks like:
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1311997/pdf/jaba00061-0143a.pdf
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Oh my gosh, that's the first time I've seen that, so I was laughing out loud.
Anyway, @OH_10381595 , welcome to the PTC Community and thanks for your contribution. July has passed, but we still appreciate your participation.
That said, Mathcad Prime has a lot of documentation features, and per the challenge guidelines, following along with your worksheet would be more of a pleasure if you incorporated some of them, like text boxes.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
We published Dave's solution blog article! And distributed badges. Thanks to everyone who participated!
https://www.mathcad.com/en/blogs/community-challenge-spherical-triangle
(Dave gave a hint that in September we'll have something from the electrical engineering domain.)
Quick reminder that we'd really like to see people's worksheets and not just screenshots of worksheets!