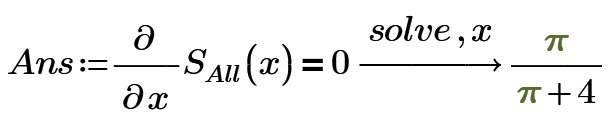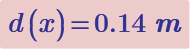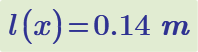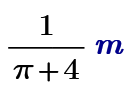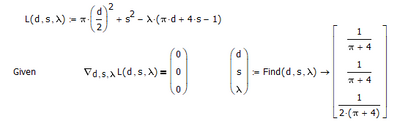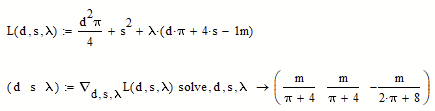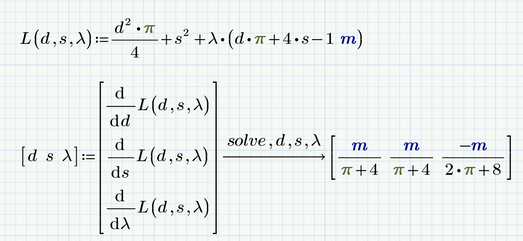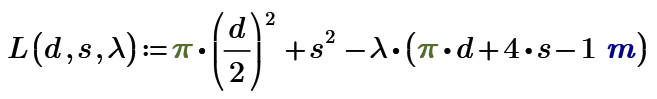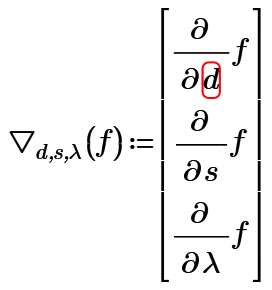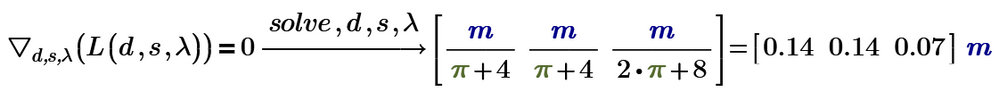- Community
- Mathcad
- Mathcad Tips
- Mathcad Community Challenge May 2022 - An Isoperim...
- Subscribe to RSS Feed
- Mark as New
- Mark as Read
- Bookmark
- Subscribe
- Printer Friendly Page
- Notify Moderator
Mathcad Community Challenge May 2022 - An Isoperimetric Geometry Problem
The first two challenges were biased towards mechanical engineering. May’s challenge pertains to geometry.
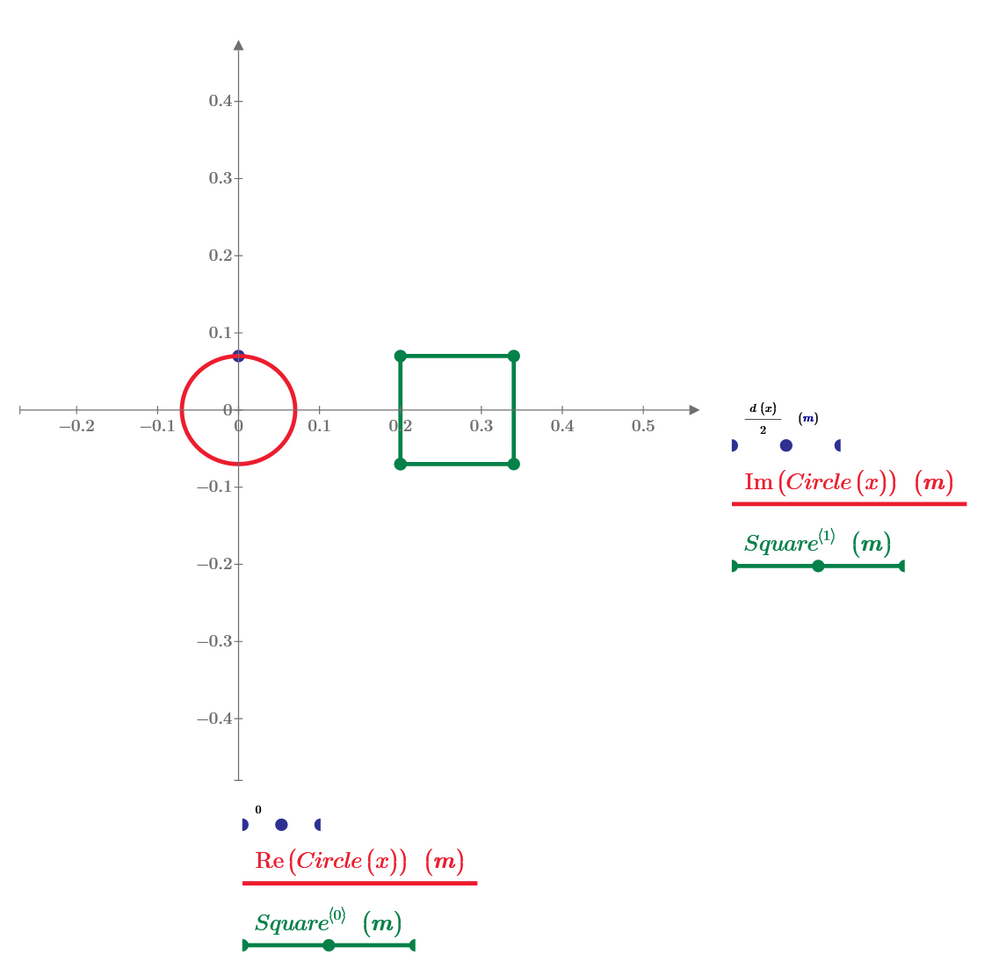
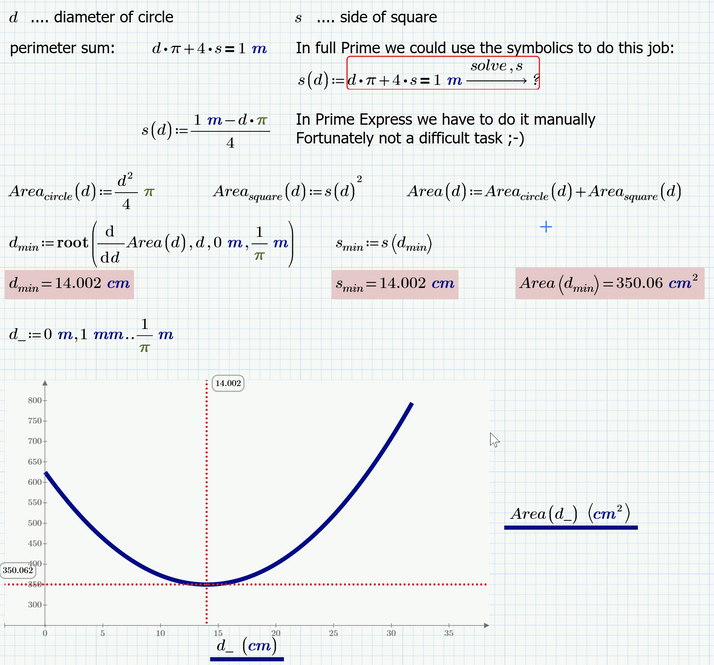
Create a worksheet in which you calculate (1) the diameter of a circle and (2) the length of a side of a square that yields the minimum combined area for a combined perimeter of 1 meter.
This is an optimization problem. What tools within Mathcad can provide you with a result?
Optional: How can you depict the results? Can you use a 2D plot or Chart Component to visualize the answer?
Find the Mathcad Community Challenge Guidelines here!
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Good solution. But it won't run in Express (no symbolics, no polyroots)
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
@Fred_Kohlhepp wrote:
Good solution. But it won't run in Express (no symbolics, no polyroots)
Also "Minimize" (even without a solve block) is a premium function.
But the derivative operator and the "root" function are not and you can use them for a solution in Express. You just have to manually solve a simple equation 😉
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Using a more powerful software you may even visualize by creating an animation 😉
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Bit of labelling would be helpful. This is like a flaming Homer.
But Short and simple.
Attach file please.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
@ppal wrote:
Bit of labelling would be helpful. This is like a flaming Homer.
But Short and simple.
Attach file please.
Moe is using real Mathcad and this seems to be a Prime only challenge. Nonetheless I would vote for his solution being the winner.
BTW, because Moe's nice compact solution is using Lagrange and the Nabla operator - is the Nabla operator now finally available in Prime 8 or is it still missing?
We could make Moe's solution even a bit more compact by using the symbolic "solve" instead of evaluating the solve block symbolically (which is something not allowed to do in Prime anyway).
It could even be made a one-liner (but I wouldn't suggest doing so):
If the Nabla operator still is not available in Prime, you would have to do it the hard way
As usual Primes infamous auto-labeling bug required to manually re-label some variables to make it work.
I seem to remember to have read that PTC planned to implement a partial derivative operator. While being only an optical display thing it would be appreciated. Is it already implemented in Prime 8 or was I just reading the roadmap for future versions?
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Thats disappointing! (I assume the pic is from Prime8 )
And how about the partial derivative operator?
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Yes, sorry, but as Werner indicates, I am using Mathcad 15. I remain firmly in the camp of "I'll switch to Prime when it can do everything 15 can do".
Very nice Flaming Homer reference, btw.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
@MoeSzyslak wrote:
"I'll switch to Prime when it can do everything 15 can do".
Never?
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Hi
MATHCAD 15
Converted to Prime 8
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
I knew that the "grad" operator was available in the original Mathcad, but I haven't seen it in Prime. Yet you show it in the Prime solve block, with a message that it isn't available.
So how did Prime execute the solve block?
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
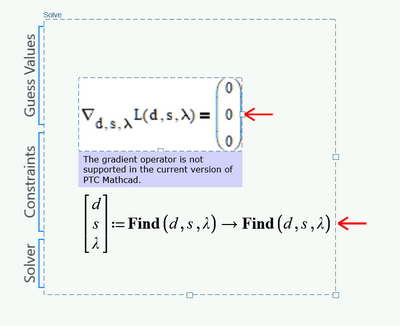
It didn't - its lying and cheating
This is what it really does when you ask it to recalculate:
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
So how did Prime execute the solve block?
The converter simply inserted a picture of the Mathcad 15 region.
Prime did not execute the solve block. As usual for Prime it stores the results of the last calculation within its file and displays them when you open a file. The file is not recalculated automatically when you open a file (as is the case in MC15 with auto-calc on). So the result you see is the result of the last calculation done in MC15 by the converter.
This is also the reason you can use Prime Express as a reader for Prime files which use premium functions. You see what the sheet looked like in full Prime but when you try to recalculate, the premium functions will fail.
So see in ppal's answer that the recalculation in Prime yields just "Find(...)". Actually its an empty solve block without any constraint and as we know Prime won't allow to evaluate a solve block symbolically.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
I opened in mathcad 15
Get errors:
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
This worksheet from 11th version of regular Mathcad.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
With animation!
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Thanks to everyone for your contributions; Dave will be reviewing them in short order since May is now over. I'm hoping for some good discussion and learnings to come out of it!
(Badges will also come soon.)
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
No June Challenge??
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
It's bimonthly, so there's been a January, March, and May challenge... and next there'll be a July.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
Badges have been distributed to valid entrants; Dave's blog on the challenge has also been published to Mathcad.com: https://www.mathcad.com/en/blogs/community-challenge-isoperimetric-problem
Great job!
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
So, it seems that my entry was not "valid" because it required Mathcad 15. Alas.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
The last bullet point of the guidelines thread says as much that it's a Prime-based challenge.
- Mark as Read
- Mark as New
- Bookmark
- Permalink
- Notify Moderator
I didn't use MathCAD, but having seen the solution to the original problem which has the diameter of the circle equal to the side-length of the square, I used a pencil to prove that if you share any fixed length of perimeter between a regular polygon and a circle, the circle which minimises the total area is the inscribed circle of the polygon. Curious...