- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
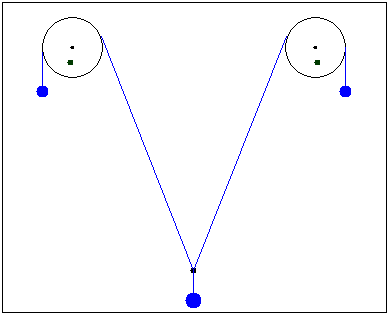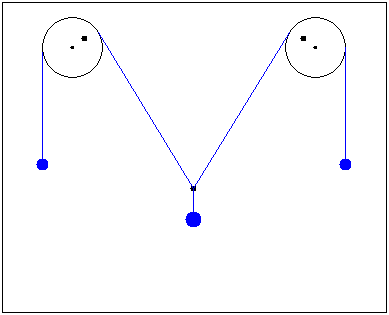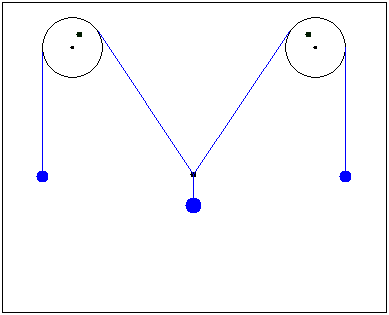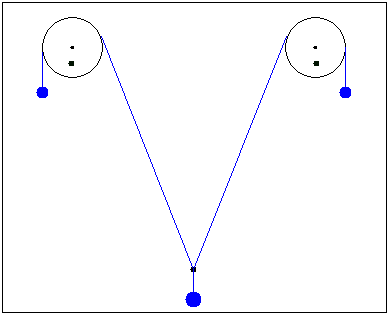
2 blocks & 3 mass
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
2 blocks & 3 mass
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
F.M. написал(а):
Beautiful, .... but the woman ... the one of the photo, is even more ...
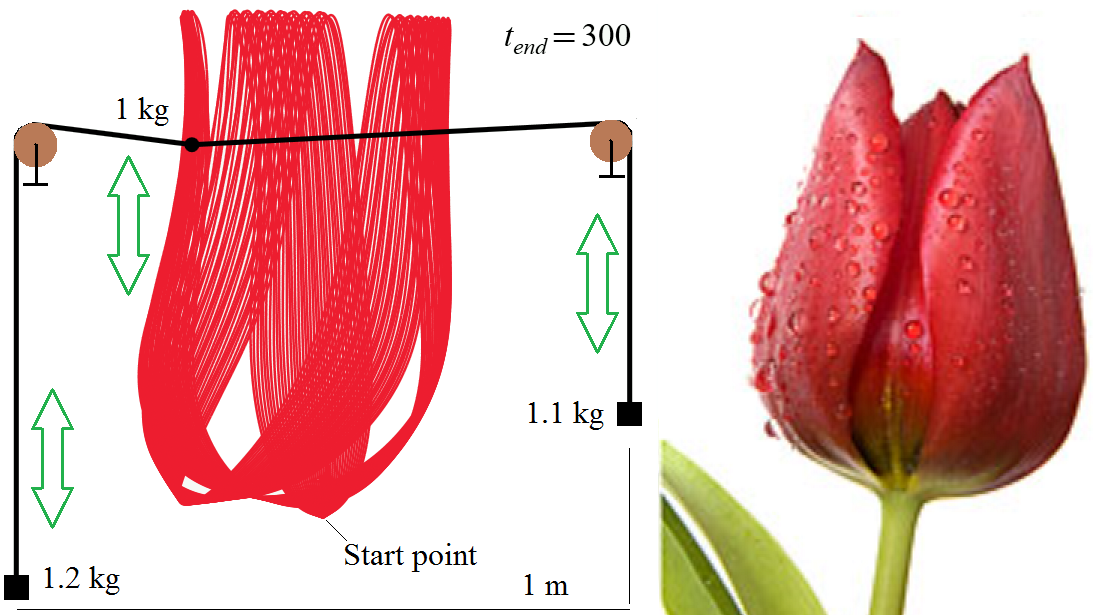
Woman and Flowers!
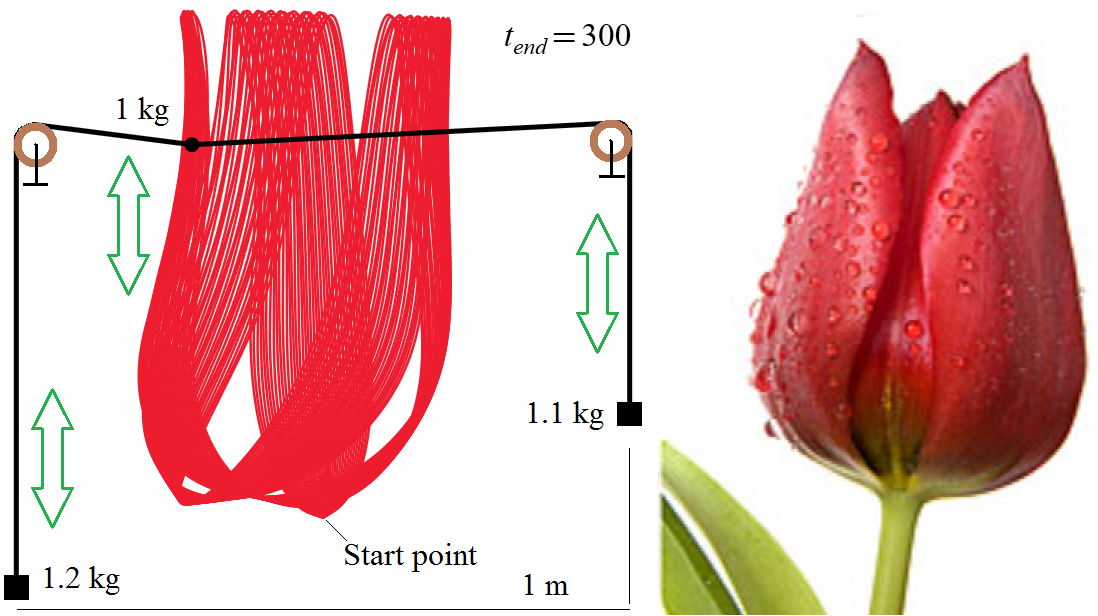
You can change L, masses, start point and get new woman, flowers etc!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Wouldn't it be better, to study the geometrical relationships before starting calculation?

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Valery,
Can we describe the problem the following way?
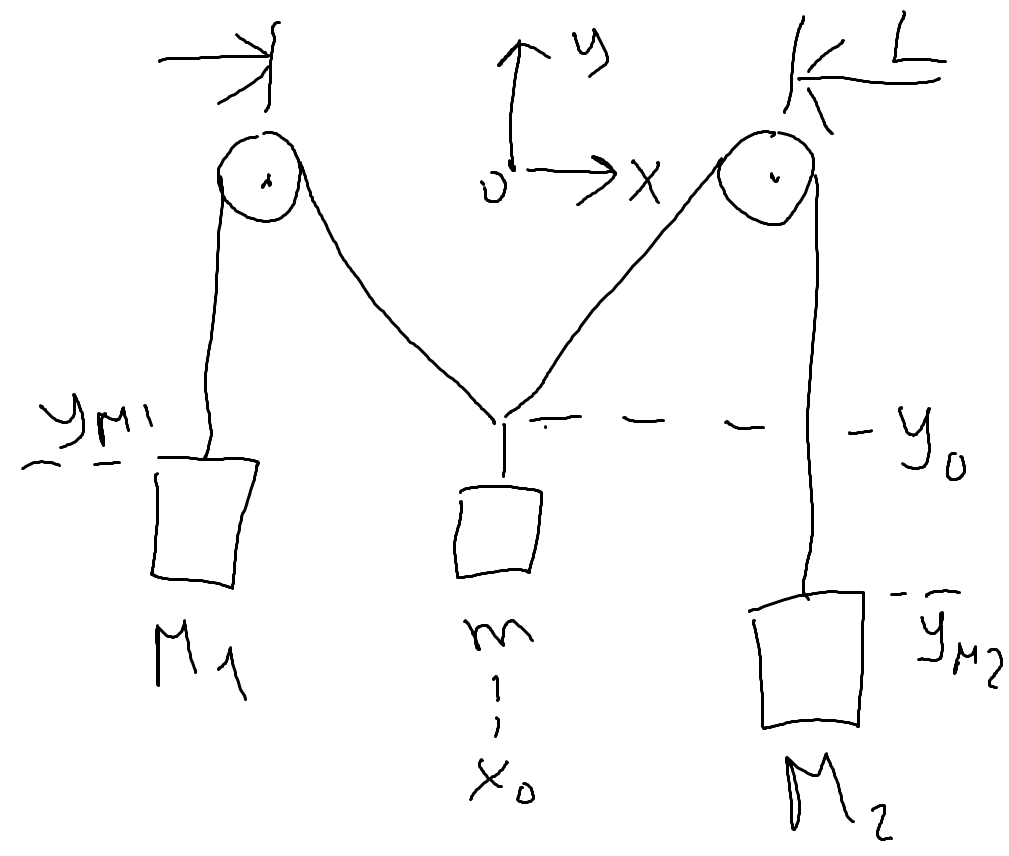
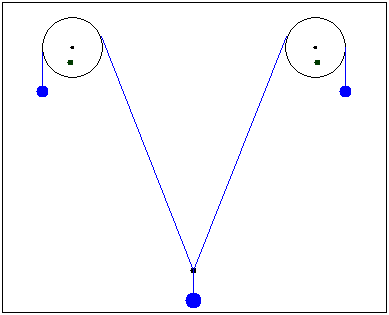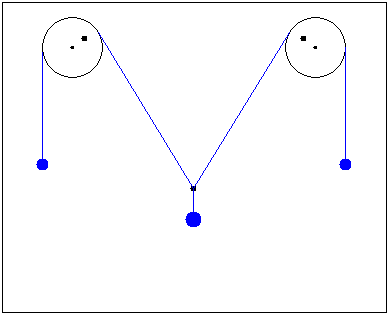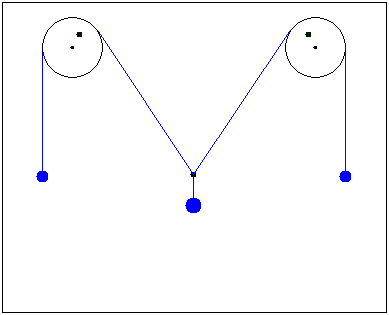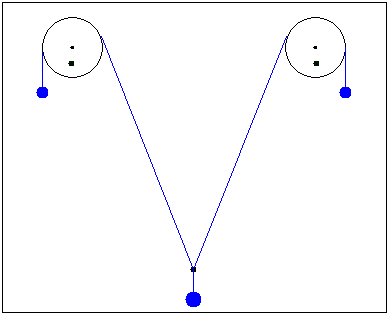
The material system consists of five bodies: the masses M0, M1, M2 and the fixed disks' masses μ1 and μ2, of equal rays r. The wire is inextensible and, by chance, it does not creeping.
Determine the system motion and the tension in the wire.
Can we choose the location of the reference system's origin, at our discretion? For example so:
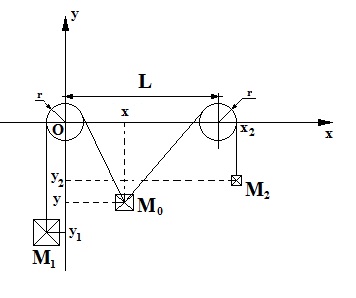
or is it fixed at L/2?
Thank you
F. M.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi F.M.
I guess it's fixed at L/2 and y0.
After releasing the weight m0 at this position, the system finds its equilibrium.
Putting the center of the first disk to the origin of the coordinate-system would be advantageous for solving with Lagrangesche Formalism.
The equations should be more simple than.
Viel Erfolg!
Volker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Salve V. L., in fact I will use the Lagrange equations.
We usually choose the origin of the axes in such a way as to make the equations as simple as possible. Valery put it in (L / 2, 0) not in (L / 2, y0). This last is your choice.
Viel Spaß
F. M.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You're right.
I think too it's the best way to choose the origin like you suggested.
Now I try the formalism.
Cappucino now ![]()
Espresso Lagrangesche![]()
tanto divertimento
Volker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Tried to use the Lagrangesche Method.
creating the differential EQN for the x-direction is ready, but it's very large. (it took a time of 30 minutes!)
Now there is to do the same for the y-direction.
see attachment please.
I'm not sure if both equations will work in a solve block.
What generalized koordinates can we choose for the Lagrangesche, that the equations become more comfortable and smaller?
Maybe with angles?
I really don't know and it seems to me that a solution here with Newton is necessary.
Viel Erfolg!
Volker
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Volker!
But es ist zu komplizirt for me.
I think we must begin with the static task with r=0 (warum nicht?).
It will be a key to solve the dynamic task.
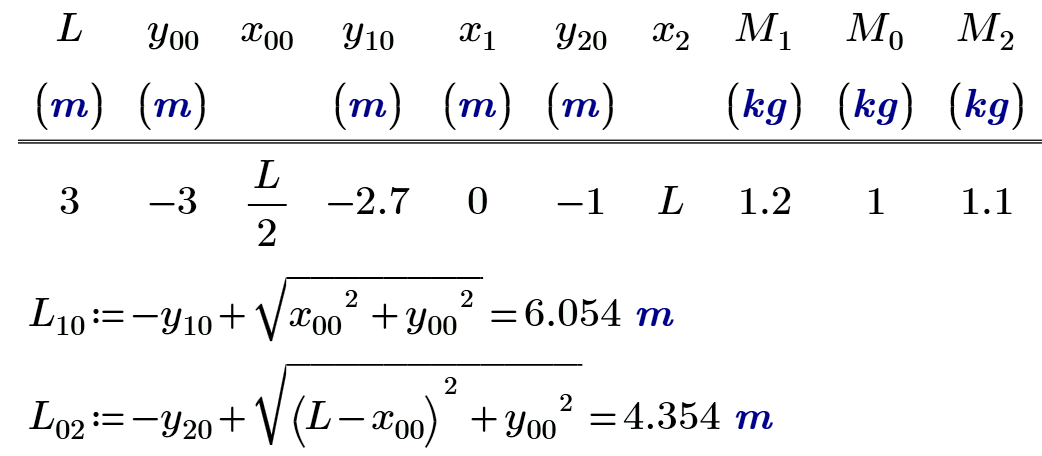


- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
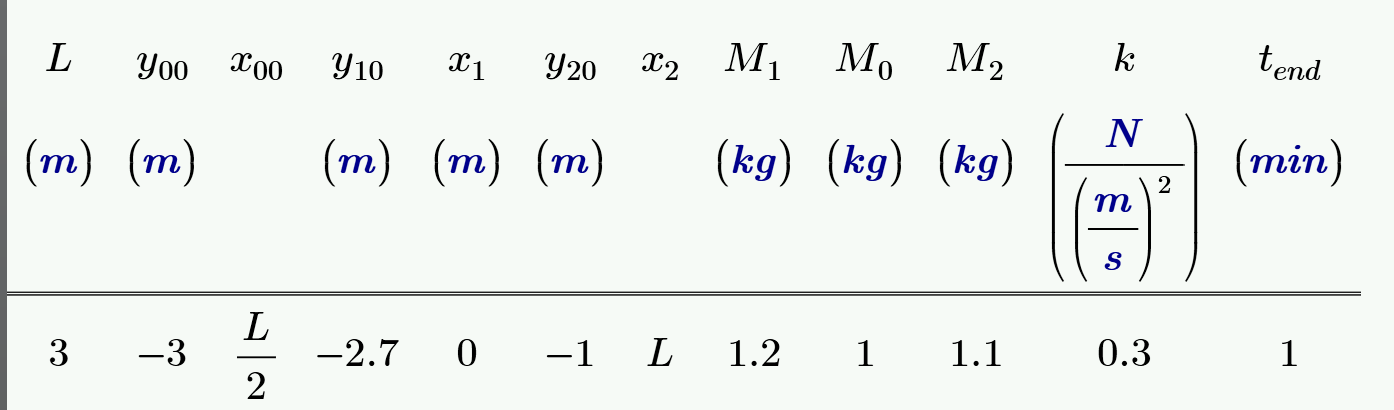

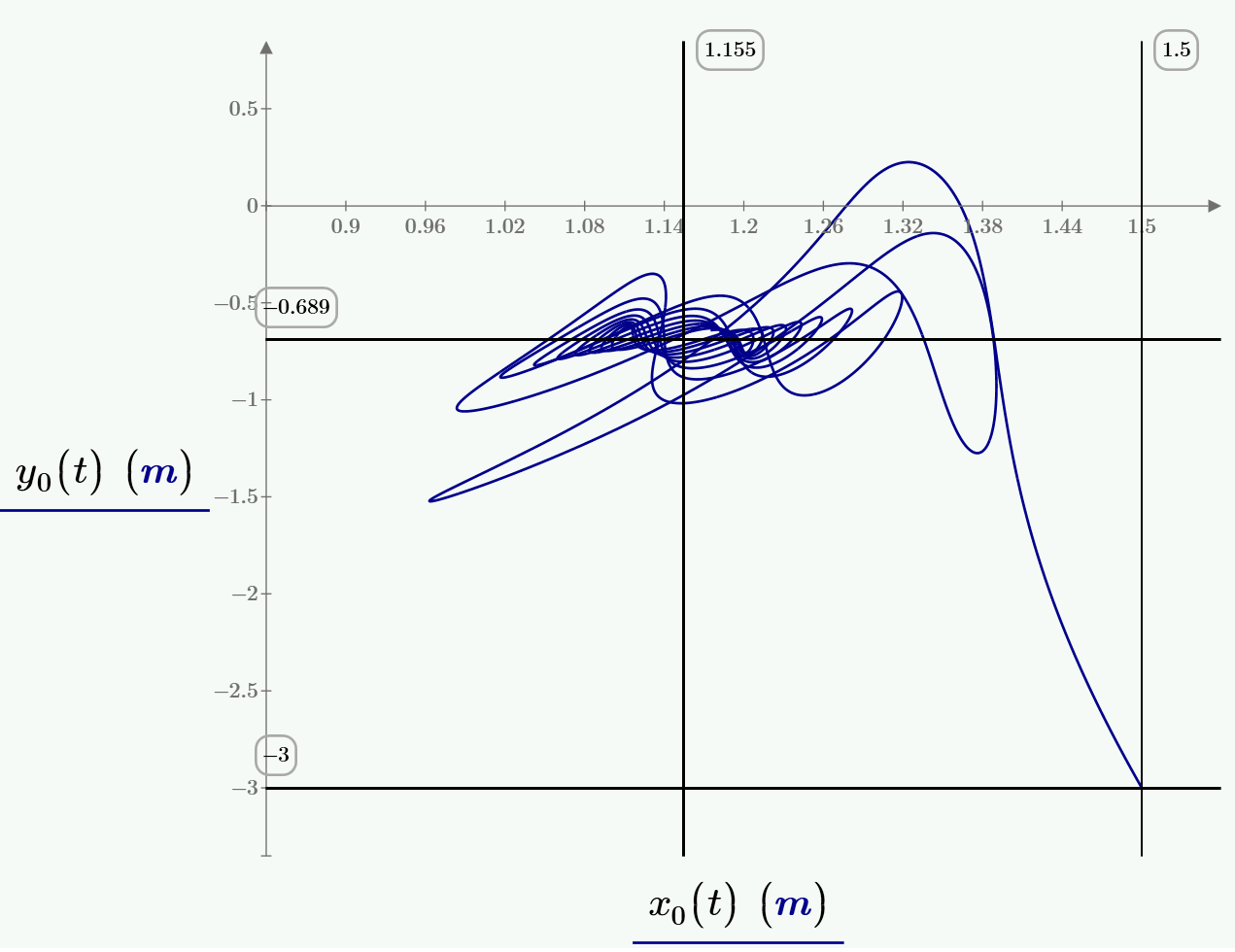
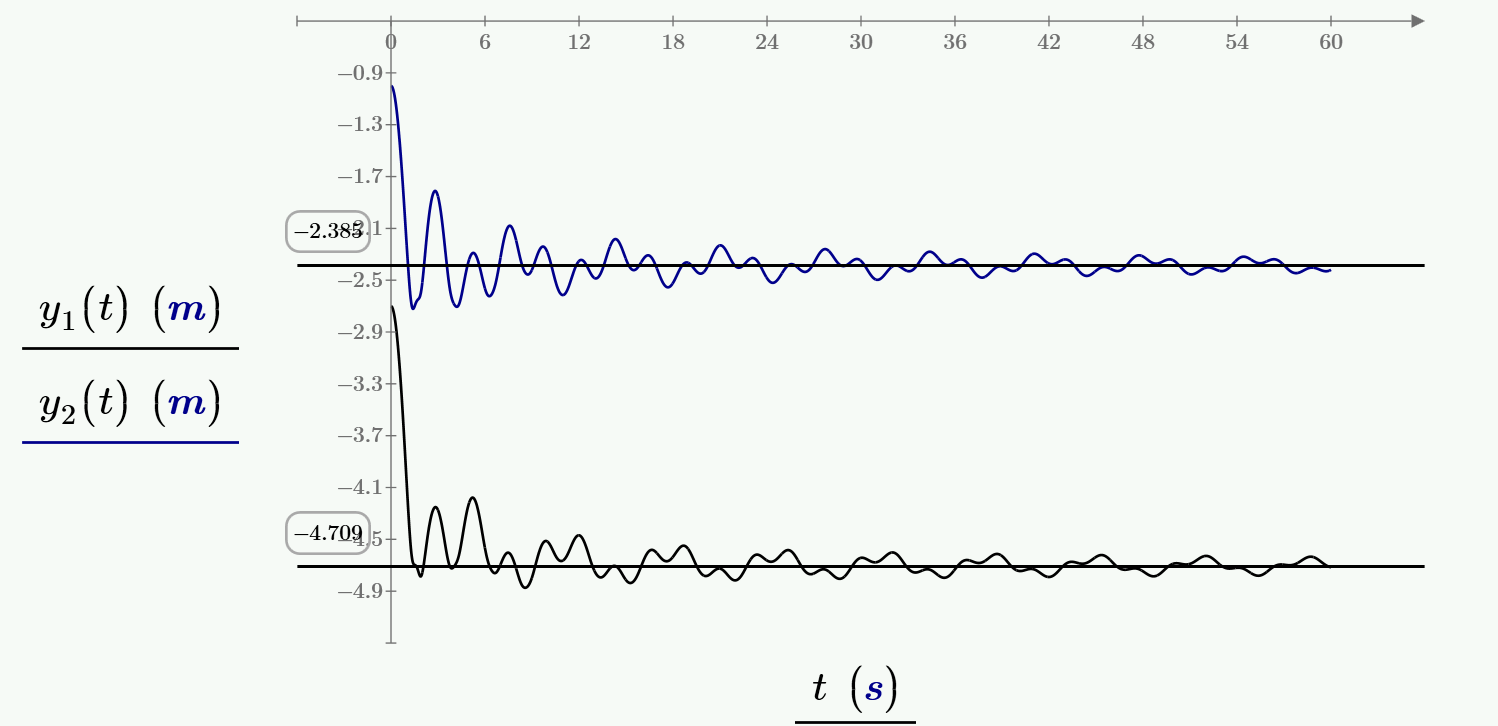
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Strictly speaking you haven't implemented the damping correctly here! If the damping force is proportional to velocity squared (or velocity*|velocity|) then you need to calculate the damping force using the resultant velocity and then resolve that along the x and y axes. This will not be the same as calculating x and y damping forces using the separate x and y components of velocity, in general.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens написал(а):
Strictly speaking you haven't implemented the damping correctly here! If the damping force is proportional to velocity squared (or velocity*|velocity|) then you need to calculate the damping force using the resultant velocity and then resolve that along the x and y axes. This will not be the same as calculating x and y damping forces using the separate x and y components of velocity, in general.
Alan
Thanks, Allan!
I know it but we use one simple model!
Help please here Sheets Mathcad 15 and Prime - one bug
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Alan,
if I understood you right, you meant this?
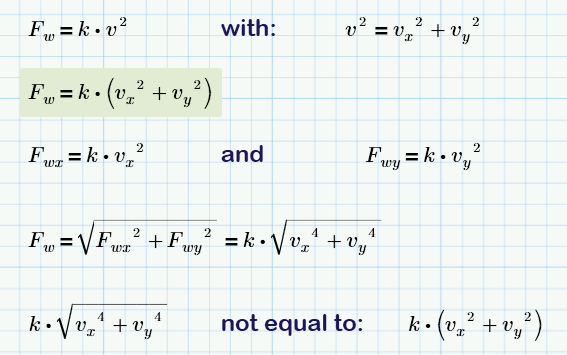
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Volker, Yes. We should have Fwx = Fw*cos(theta) and Fwy = Fw*sin(theta) where Fw is as you've defined it and theta = tan^-1(vy/vx).
However, this would only be of importance in a real problem - it doesn't matter too much in a toy problem. It's just the pedant in me pointing it out!!
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens написал(а):
Volker, Yes. We should have Fwx = Fw*cos(theta) and Fwy = Fw*sin(theta) where Fw is as you've defined it and theta = tan^-1(vy/vx).
However, this would only be of importance in a real problem - it doesn't matter too much in a toy problem. It's just the pedant in me pointing it out!!
Alan
One compromise:
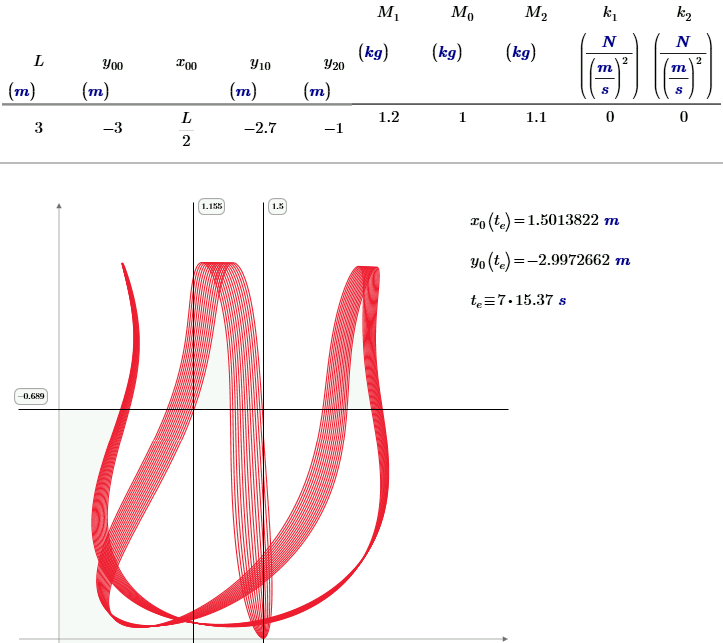
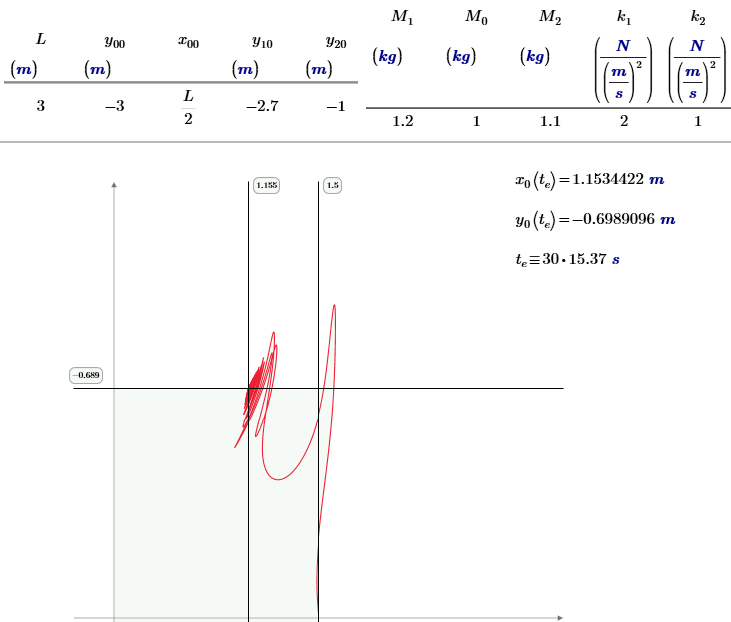

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
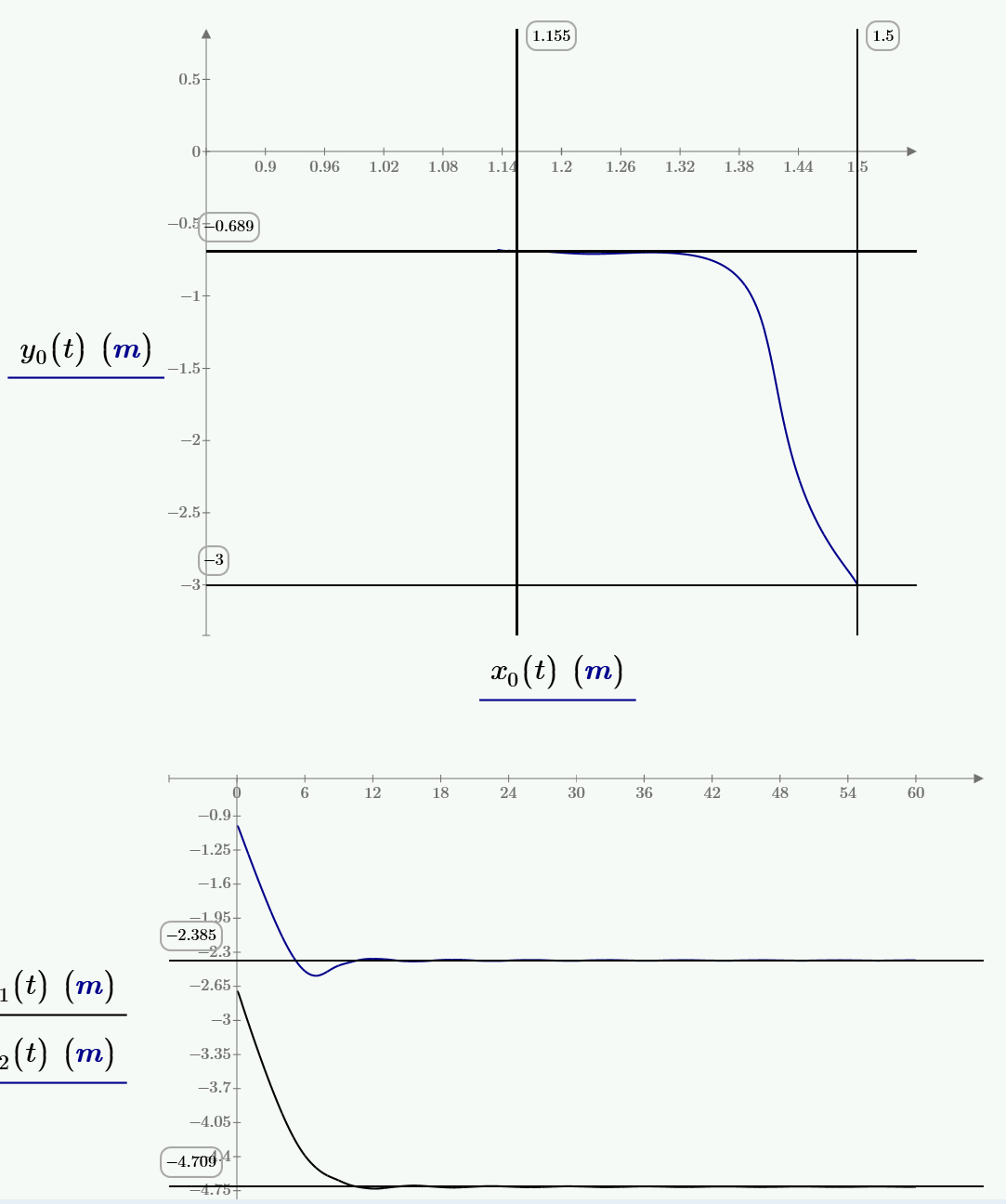
Ok. I might as well show my solution using damping in the form I mentioned previously. Note that my worksheet is M15, and first does a static equilibrium calculation, then does the dynamics (only the dynamics part pictured below).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Alan!
But a solution without an animation is not solution.
A solution with one animation is not solution too.
Tree animations are good!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
Thanks, Alan!
But a solution without an animation is not solution.
Ok. Here is a (not very exciting!) animation:
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, Alan!
I do not see an animation.
We must convert avi to mov and than input it here.
Attach please the avi file - I will convert it and put here!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens написал(а):
Ok Valery, thanks. avi file attached.
Alan
Sorry. The solution with animation but without trajectory is not full solution ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Animating a simpler task in Smath Studio
http://en.smath.info/forum/yaf_postst973_Animation-double-pendulum-and-a-pendulum-on-a-spring.aspx
Fluctuations of three loads .The system consists of two extreme loads mass m1 and medium load mass m2 (2m1> m2).If the average load deviate from the equilibrium position, the system begins to oscillate.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fridel Selitsky написал(а):
Animating a simpler task in Smath Studio
http://en.smath.info/forum/yaf_postst973_Animation-double-pendulum-and-a-pendulum-on-a-spring.aspx
Fluctuations of three loads .The system consists of two extreme loads mass m1 and medium load mass m2 (2m1> m2).If the average load deviate from the equilibrium position, the system begins to oscillate.
Sorry. The solution with animation but without not simple, interest, fine trajectory is not full solution!

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov schrieb:
One compromise:
Maybe we don't need a compromise:

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Zu compliziert for me
Sergey Dovlatov about one compromise:
"Дело происходило в газете "Новый американец". Рубин и Меттер страшно враждовали. Рубин обвинял Меттера в профнепригодности. (Не без основания). Я пытался быть миротворцем. Я внушал Рубину: — Женя! Необходим компромисс. То есть система взаимных уступок ради общего дела. Рубин отвечал: — Я знаю, что такое компромисс. Мой компромисс таков. Меттер приползает на коленях из Джерси-Сити. Моет в редакции полы. Выносит мусор. Бегает за кофе. Тогда я его, может быть, и прощу."
It happened in the newspaper "New American". Rubin and Metter were terribly hostile. Rubin accused Metter of being unfit for work. (Not without reason). I tried to be a peacemaker. I suggested to Rubin: "Eugene!" A compromise is needed. That is, a system of mutual concessions for the sake of the common cause. Rubin answered: - I know what a compromise is. My compromise is this. Metter crawls on his lap from Jersey City. Wash floors in the office. He takes out the garbage. Running for coffee. Then I, perhaps, will forgive him.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Did you try it?
You cant say its zu kompliziert for me without trying it!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Volker Lehner написал(а):
Did you try it?
You cant say its zu kompliziert for me without trying it!
You are right.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Volker!
But es ist zu komplizirt for me.
I think we must begin with the static task with r=0 (warum nicht?).
It will be a key to solve the dynamic task.
And meanwhile, i think so too.
I try to solve it now with Newton by myself.
Let's see what F.M. makes with the Lagrangesche.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I do not show the picture with solution!
You can see the attach or not see - try to create yourself and compare than!