Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
4x4 Magic Square.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
4x4 Magic Square.
Hello, Everyone.
Is it possible to solve M matrix, the above ?
Thanks in advance for your time and help.
Regards.
Solved! Go to Solution.
- Labels:
-
Algebra_Geometry
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One can get quite far though:

It's just that the inequality constraint (involving M01 and M03) is not obeyed. Note that I first tried:
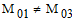
But then I got an error message saying it's not allowed inside a solve block.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
At first glance: no
Reason: your system is over-constrained. You have 16 variables to find, you can have only 16 constraints.
The requirement of a magic square (sums of all 4 rows and of all 4 columns and along the 2 main diagonals must be equal) already gives you at least 4+4+2-1=9 constraints. Now you've added 16 more constraints, totalling 25.
Another constraint from the magic square is that all your variables must be different AND in the range 1 through 16.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Apart from what Luc already wrote you would have to constraint the matrix elements to be integers - something which Mathcad is not really good at.
So I guess the better option to get a magic square is to write a program following one of the algorithms to build a magic square. There a quite some in print, ususally differing according to the magnitude of the sqare, distinguishing odd or even order and as far as I remember ther is a short algorithm dealing with squares of a mgnitude which is divisable by 4.
What exactly ist the problem you should solve for homework?
WE
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One can get quite far though:

It's just that the inequality constraint (involving M01 and M03) is not obeyed. Note that I first tried:
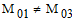
But then I got an error message saying it's not allowed inside a solve block.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your time and help, Werner and Luc. ![]()
![]()
I have just realized my question at the moment about : Pandiagonal magic square - Wikipedia, the free encyclopedia
Is it possible to solve COMPLETE MAGIC SQUARE, and How many solution in this case ?
Best Regards.
Loi.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How many solution else for COMPLETE MAGIC SQUARE does it have in this case ?
Thanks in advance.
Regards.
Loi.





