- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Adjust Bessel function to data
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Adjust Bessel function to data
Hi,
I need to adjust a Bessel function to this data. I was unable to make it and I can't discover the error. Can someone help me?
Solved! Go to Solution.
- Labels:
-
Physics
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
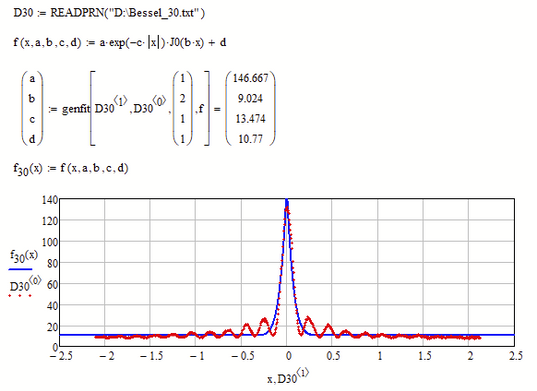
The Bessel function will not work, note that J0 does not have a flat lower bound, like your data shows.
It may help to square the Bessel function, like this:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I can't discover the error.
Which error?
Post your Mathcad or Prime sheet!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I'm trying to use the QuickSheet of Fitting nonlinear functions to data. But my problem starts when I have to define the bessel function J0. I don't have the analytic expression for the function, so I can't use the genfit.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The Bessel function J0 does not have any parameters you may twist to fit to some data.
Why do you think that you must fit with a Bessel and what modified version of Bessel do you have in mind?
Where does the problem stem from?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello,
These data are of intensity depending on the distance of a diffraction pattern. From the aspect of the curve, I think it's a zero-order Bessel function because it doesn't cancel out at the origin. I even saw an example on the forum but I didn't quite understand it because I'm a Mathcad beginner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
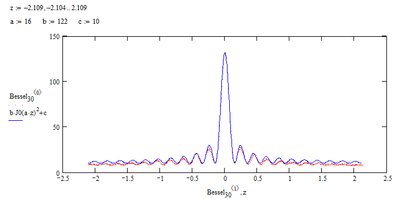
You may of course scale the Bessel in x and y direction and/or shift it, but the result sure is not satisfactory as you can see:
Maybe a damping factor of some kind is needed, but a first try with exp(-c*|x|) made it even worse:
So, unless you know a bit more about the type of function to fit, ...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
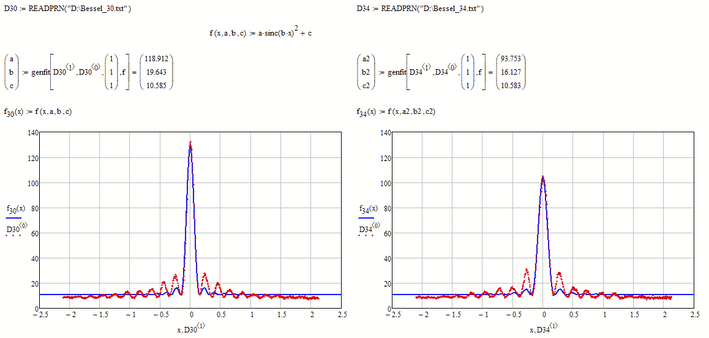
I think it might be better to fit a more standard diffraction function:
I = I0*sinc(k*x)^2
where I is your first column of data, x is your second column and sinc(x) = sin(x)/x
Having fitted I0 and k to your data you could see how k compares with the theoretical value (it’s a function of slit width, distance from slit to plane and wavelength of light),
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's the result of Alans suggestion. I had to add a parameter c for vertical displacement
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thnak you Werner_E for the help. Using your tip and LucMeekes 1'm able to fit the function
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The Bessel function will not work, note that J0 does not have a flat lower bound, like your data shows.
It may help to square the Bessel function, like this:
Success!
Luc