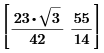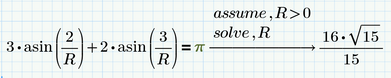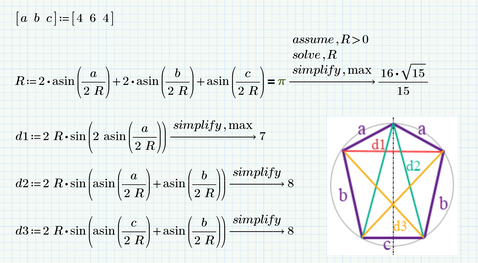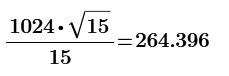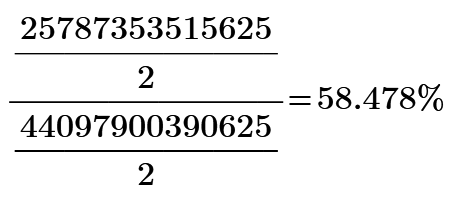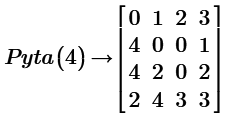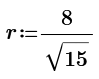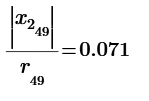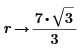Community Tip - Want the oppurtunity to discuss enhancements to PTC products? Join a working group! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
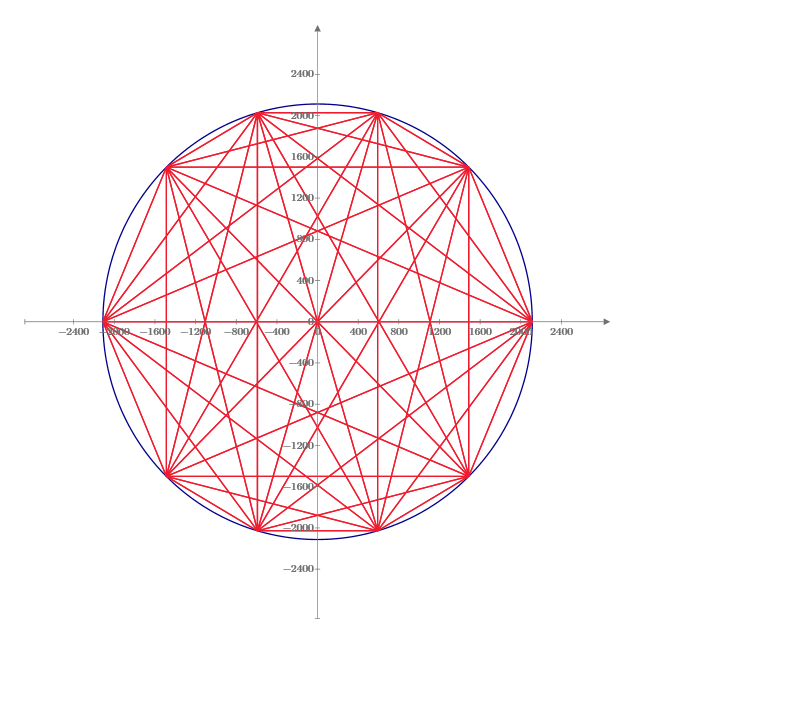
All distances of the points to be Integer
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All distances of the points to be Integer
(This is only a puzzle to fun! )
Tokoro.
All distances of the points to be Integer
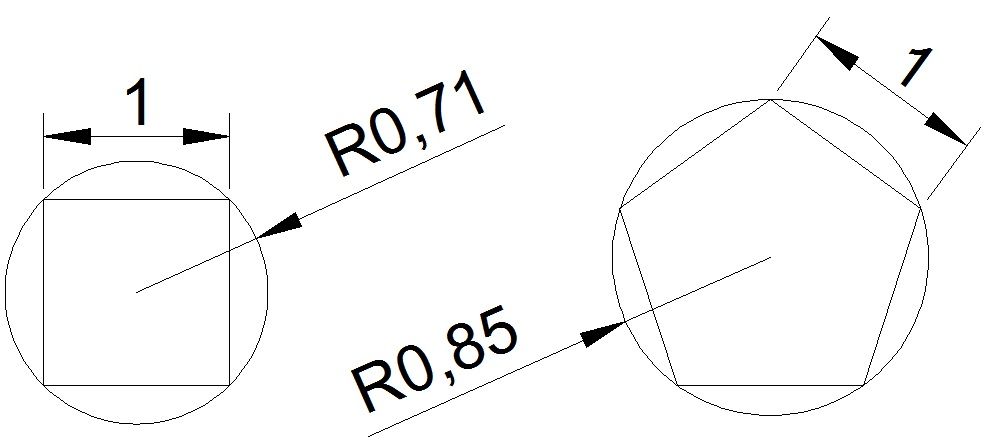
- Make a circle with its center (0,0) and radius r.
- Make five points on the circle with all distances of the points to be integer.
- The puzzle is to find the minimum of r.
- Next, the same puzzle except the number of points are 10.
- The answer of 4 points attached.
Solved! Go to Solution.
- Labels:
-
Puzzles Games
- Tags:
- puzzles
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I found the lengths 4,6,4,6,4 by trial and error until I got integer results for the diagonals.
Regards
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I'll play (The definition does not need the radius be an integer?)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
You are not free on the radius. Because the diagonals are twice the radius. Hence radius must be an integer times 1/2.
Which diagonal of which pentagram must be a diameter of the circle? There may be a solution where one diagonal or maybe even one side of the pentagon is a diameter but sure not necessarily.
Even with four points its not demanded to be a regular quadrilateral or to have any symmetries. Its just the solution shown which happens to be at least a rectangle. And I see no proof that 5/2 is the minimum for the radius in case of a quadrilateral.
I have no clue how to proof that the solution for 4 points shown really is the minimum (wrt the radius) and that not maybe an irregular quadrilateral would not lead to a smaller radius.
Nor have I any idea how to use Mathcad to help finding any solution with 5 points, let alone the minimum one.
Its clear that it suffices to demand for all distances to be rational as we then can blow up the figure as necessary to make them integer, but I don't think that knowing this is much of help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I stand corrected.![]()
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@terryhendicott wrote:
Hi,
I'll play (The definition does not need the radius be an integer?)
Correct, but I guess you overlooked that ALL distances of any two points must be integer. This includes the diagonals which in case of your pentagon are not integer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Werner
thought it was too easy
Cheers
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
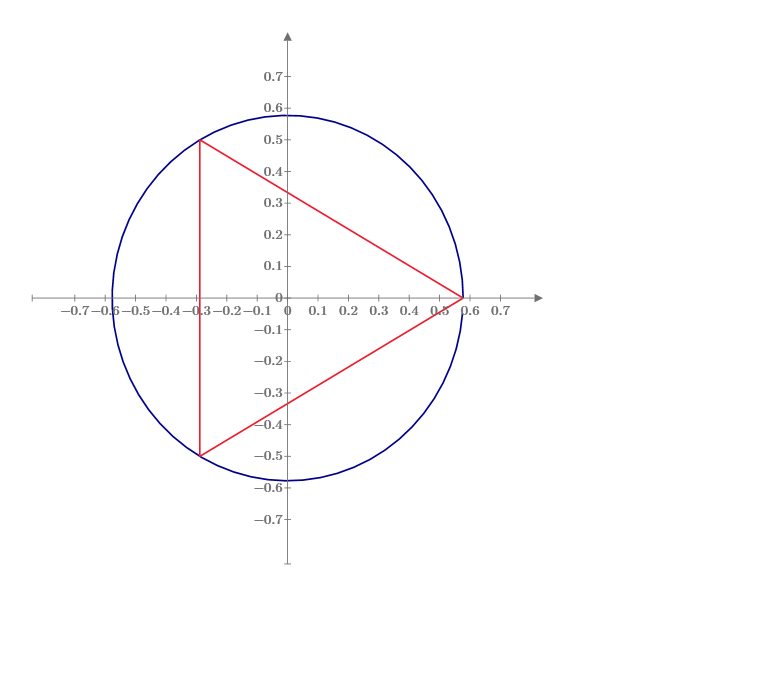
Thanks for your time to fun! Your answer is correct for 3 points.
By the way, connect all n points on the circle is good programing exercise for the students.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
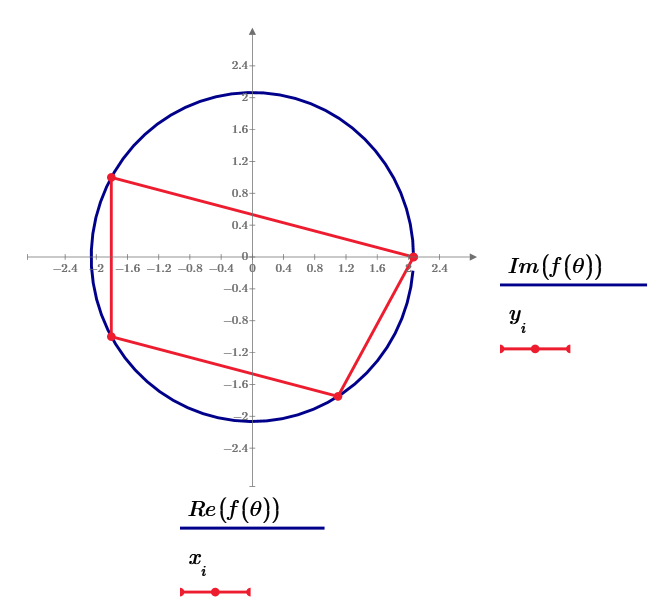
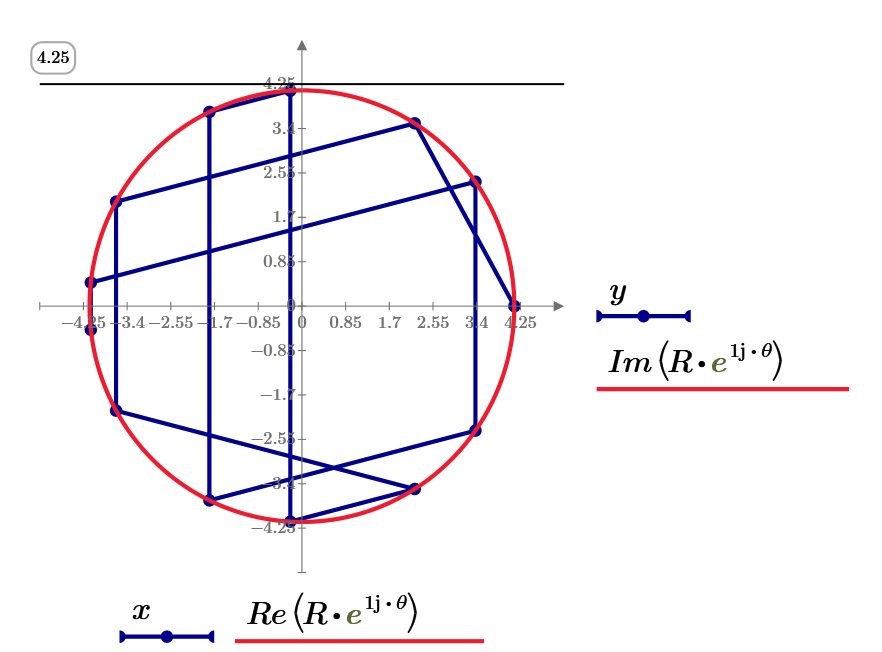
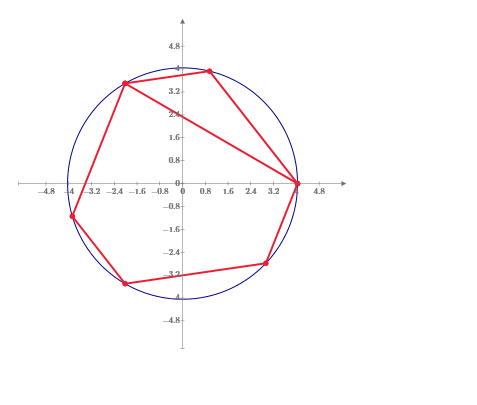
Hi,
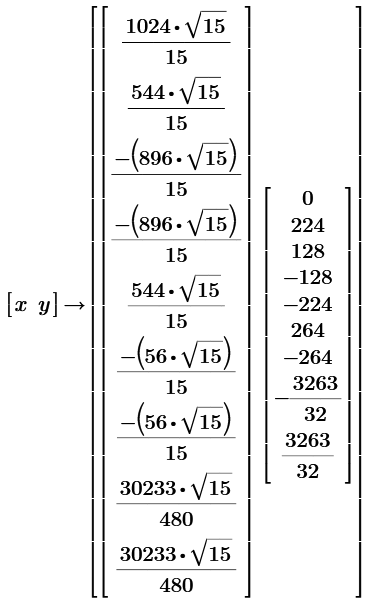
Have an answer for 5 pointed problem.
Sides are 4,6,4,6,4 in a 4.131182 radius circle.
Diagonals are 8,8,8,7,8 all integers.
Calculation sheet enclosed.
It is based on solution of intersection of two circles one centred at origin and radius R, the other centred at R,0 with radius equal to side length.
Starting with next side, place a circle of radius the length of the side and centre at last location obtain the intersection point.
Repeat this for each side.
This is repeated around the circle to get a closing angle that should equal 2 pi.
Manually ratio the closing angle to 2 pi to get the next starting radius. Just do this till maximum accuracy is obtained
Cheers Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
To be exact, that radius is 16/sqrt(15).
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
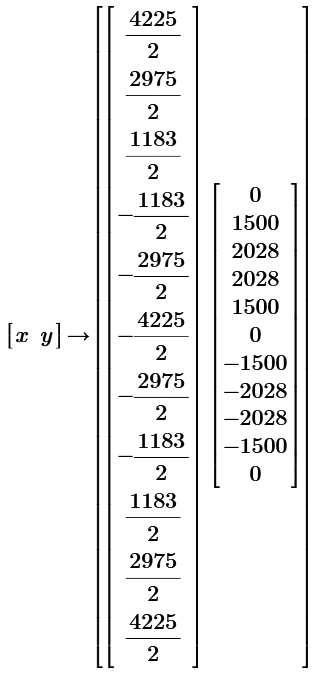
Great Solution!
But how do you get the side lengths 4,6,4,6,4 ?
Once you have decided that the sides should be of that lengths, the radius can easily be found using symbolic solve:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I found the lengths 4,6,4,6,4 by trial and error until I got integer results for the diagonals.
Regards
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
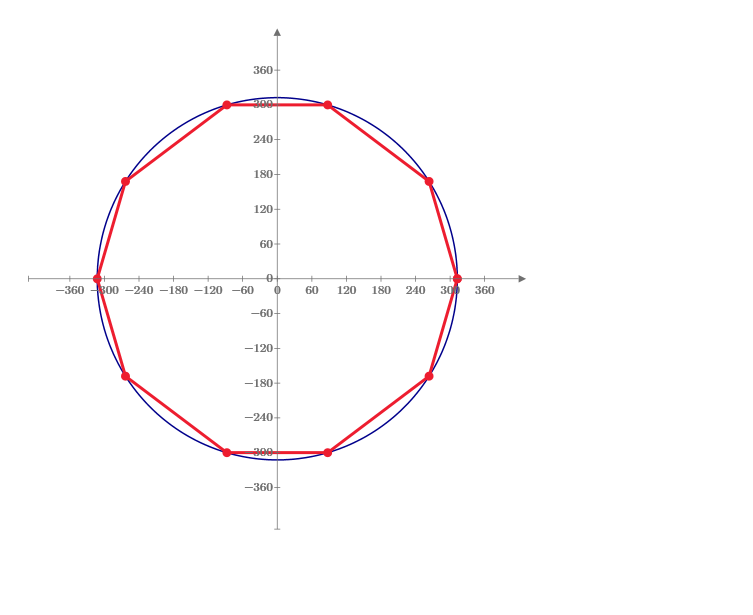
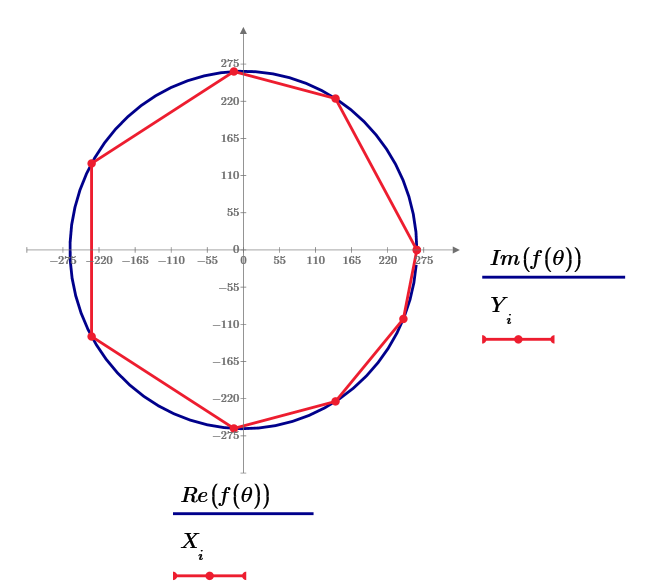
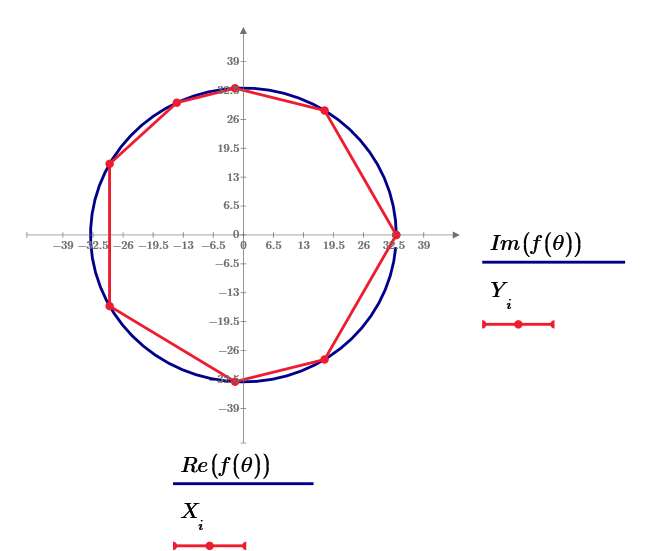
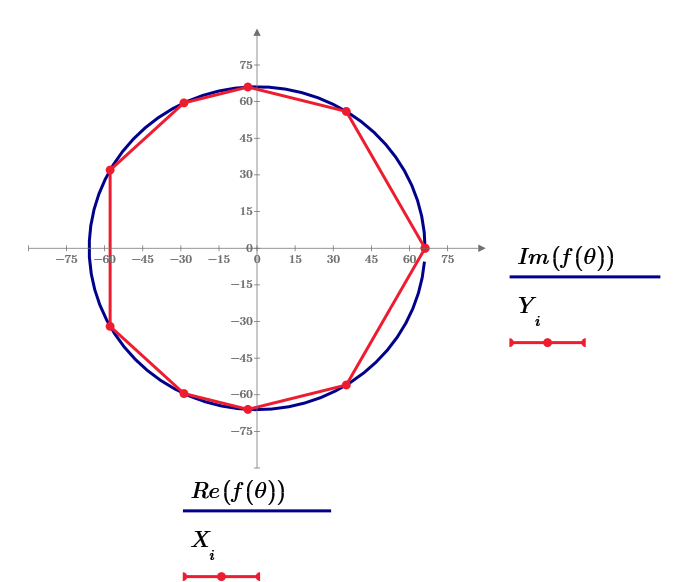
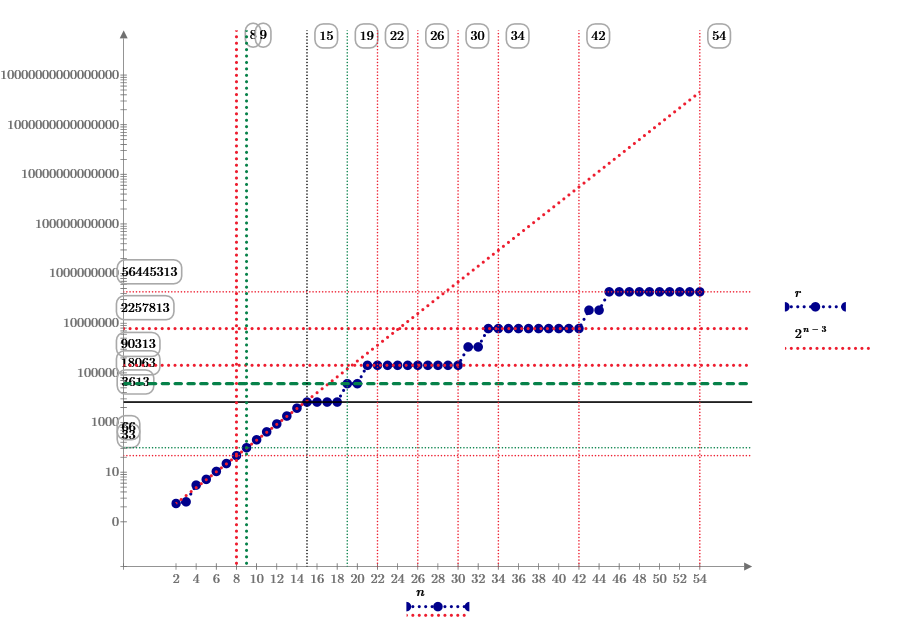
This answer of n=8 is r=
It is very large and the shape is not smart. So, the best answer should be more small.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad Prime 6.0 sheet. n=8
n=9
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
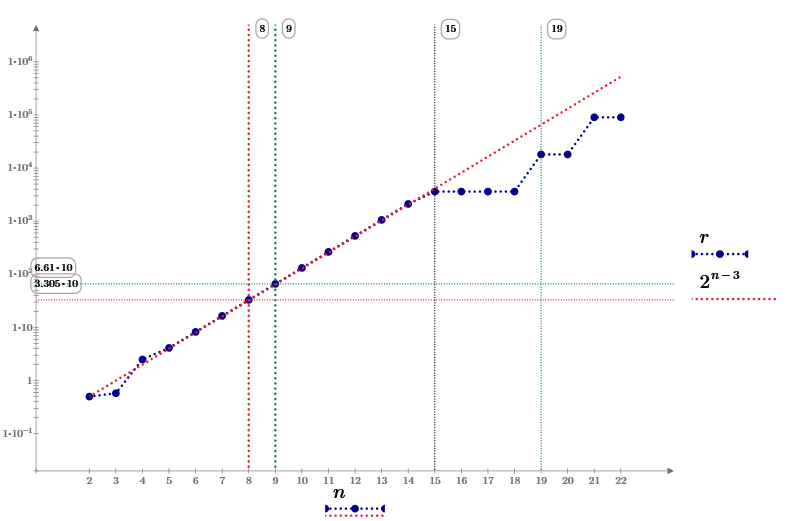
I find a new point of No.14. So the r reduced to
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
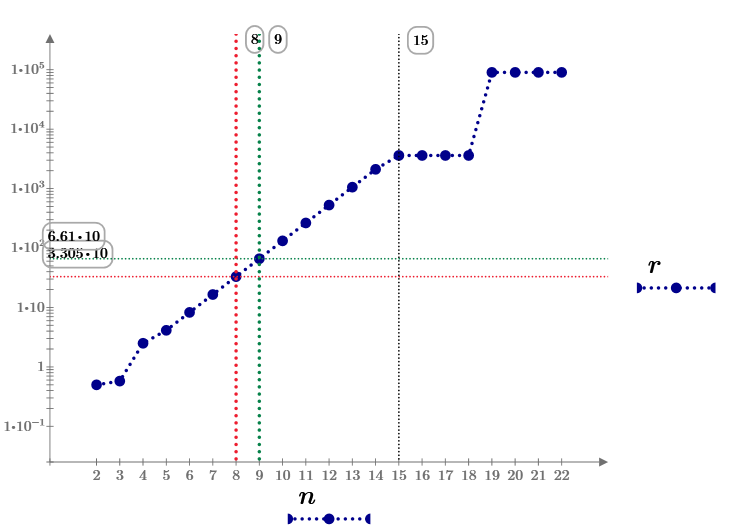
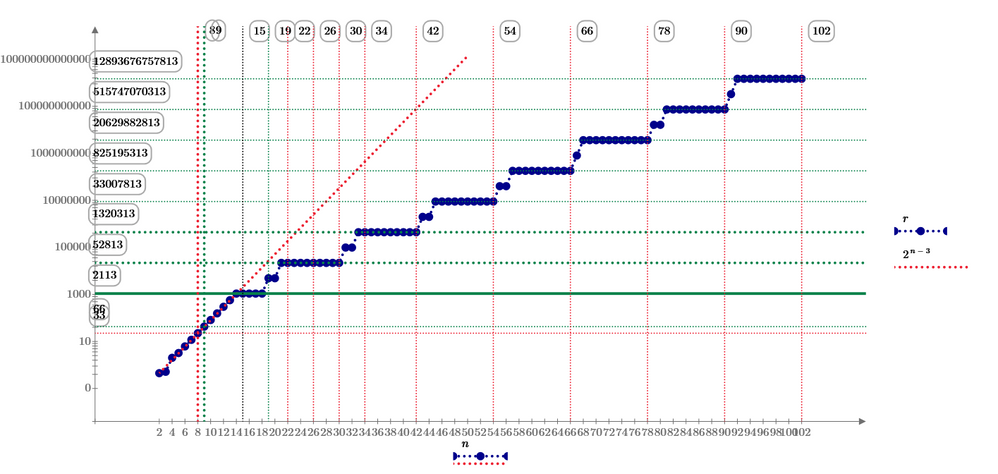
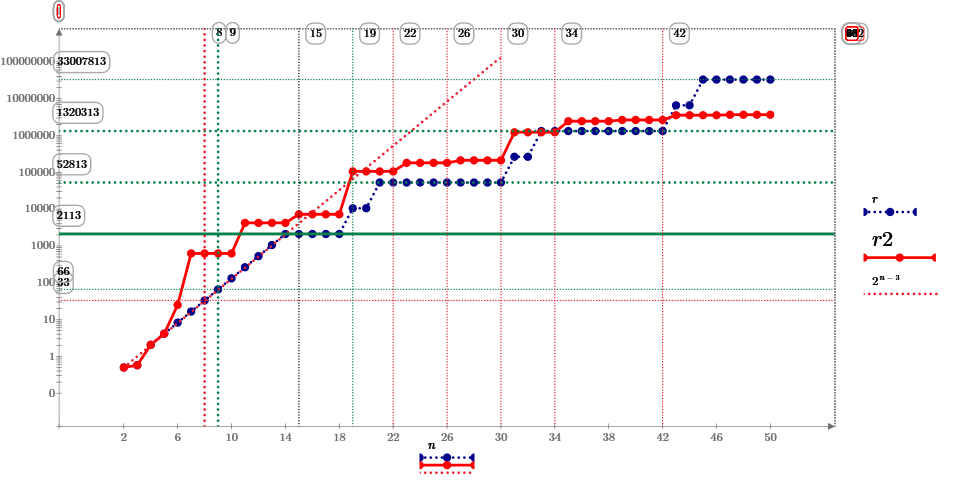
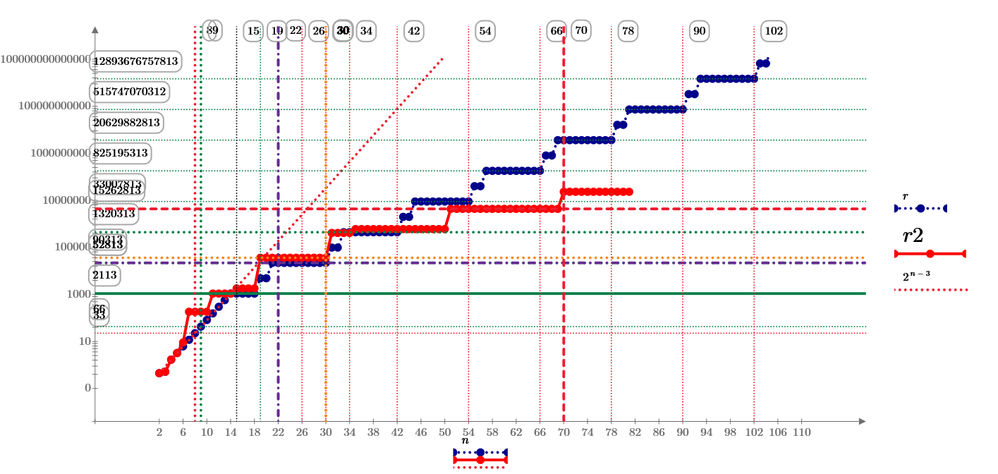
This calculation also limited by 15 digits, It is about 100 points on the circle. May be from 2 to 5 points are the best solutions.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Find the new 4 points answer.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
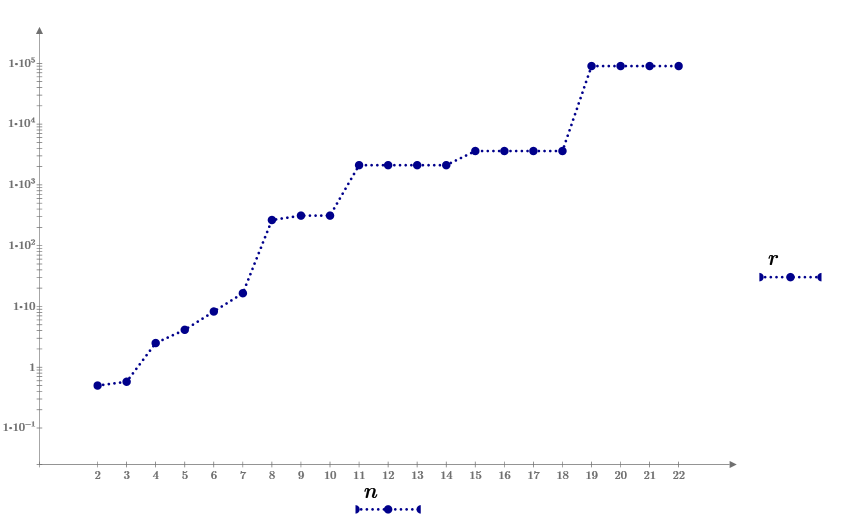
Answers of n=4 to 13. No.5 is find by terryhendicott.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
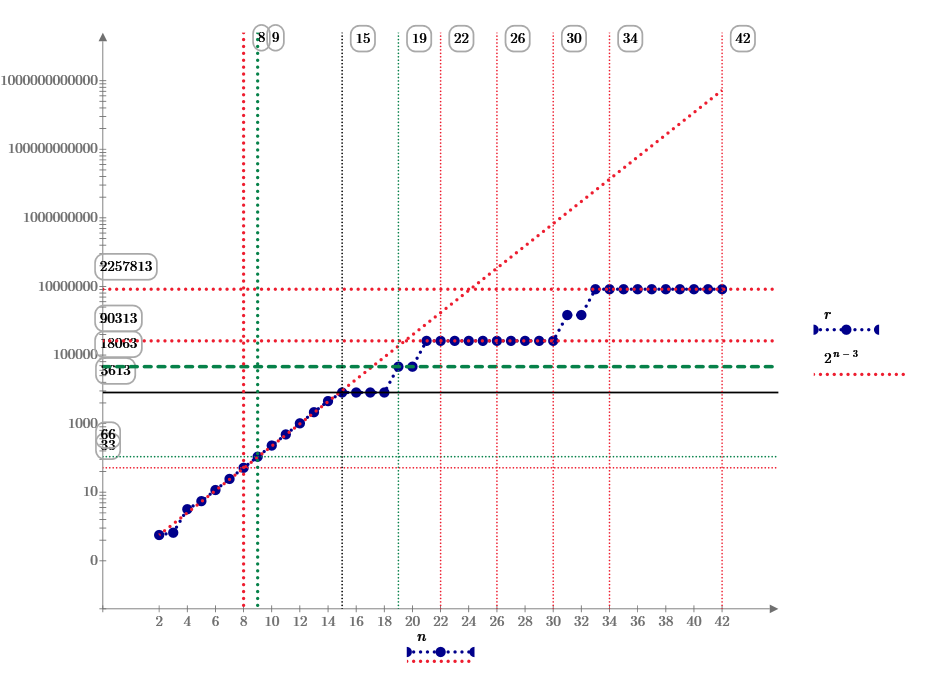
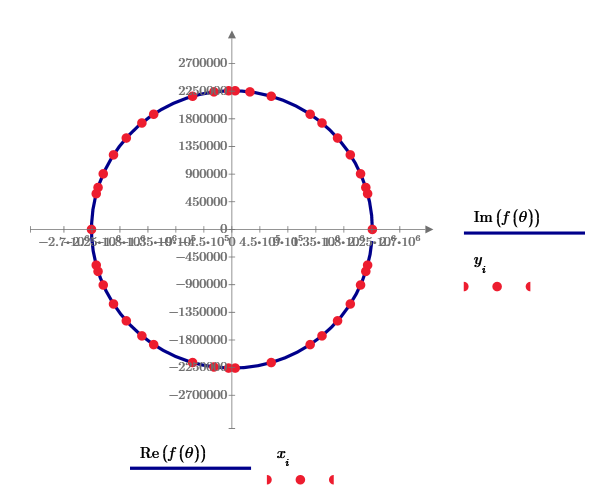
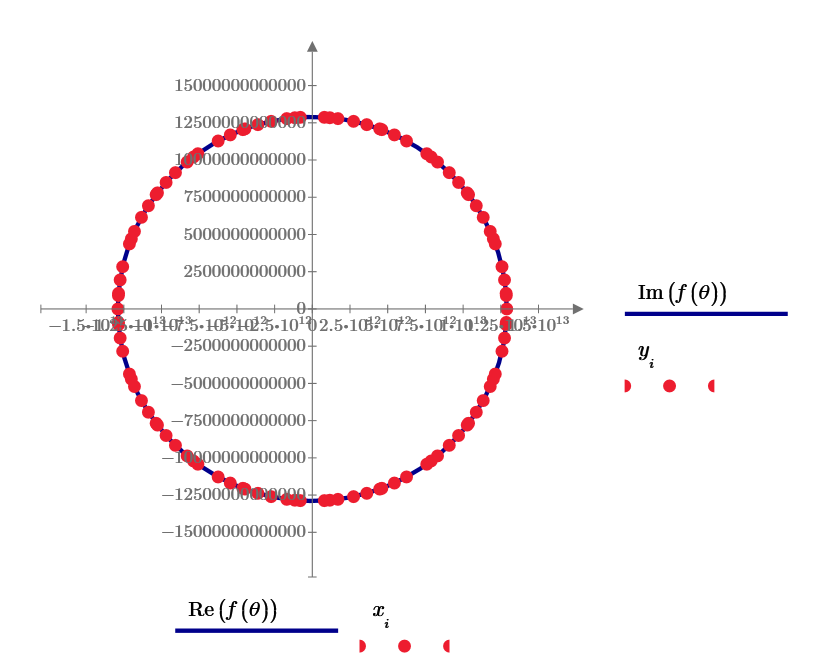
New stab series (red line) reduces to only 7% at 50 points.
(3663075,0) (-3663075,0)
(3649821,311328) (-3649821,311328) (-3649821,-311328) (3649821,-311328)
(341859,3647088) (-341859,3647088) (-341859,-3647088) (341859,-3647088)
(3596925,693000) (-3596925,693000) (-3596925,-693000) (3596925,-693000)
(723075,3591000) (-723075,3591000) (-723075,-3591000) (723075,-3591000)
(1025661,3516552) (-1025661,3516552) (-1025661,-3516552) (1025661,-3516552)
(3491709,1107288) (-3491709,1107288) (-3491709,-1107288) (3491709,-1107288)
(1672419,3259008) (-1672419,3259008) (-1672419,-3259008) (1672419,-3259008)
(3244899,1699632) (-3244899,1699632) (-3244899,-1699632) (3244899,-1699632)
(3219171,1747872) (-3219171,1747872) (-3219171,-1747872) (3219171,-1747872)
(1774749,3204432) (-1774749,3204432) (-1774749,-3204432) (1774749,-3204432)
(2040675,3042000) (-2040675,3042000) (-2040675,-3042000) (2040675,-3042000)
(2348931,2810808) (-2348931,2810808) (-2348931,-2810808) (2348931,-2810808)
By H. Fujiwara.
- Tags:
- puzzle
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- Prime_6.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Today, Suzuki find the new smallest answer for n=5 to 18.
n=5 The answer is.
[r 0],7,5,3,5,3.
n=6. Same r and add