Skip to main content
-
-MFra-21-Topaz II
21-Topaz II
September 18, 2019
Question

Bode trap

  • September 18, 2019
  • 1 reply
  • 1863 views

Hi,

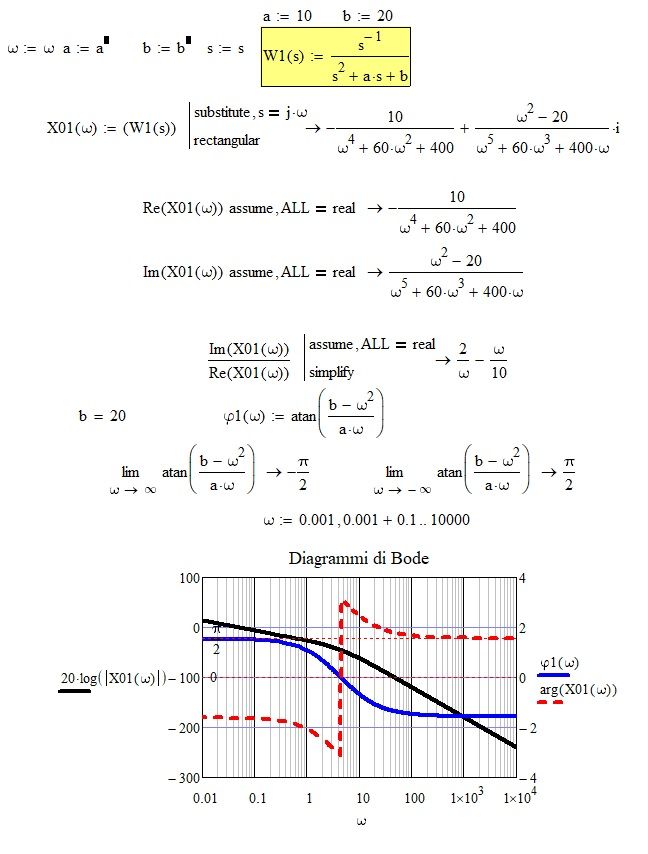
A friend asked me for a phase diagram of a transfer function (see photo and file). I distractedly used the arg(Im(W (iĻ‰))/Re(W(iĻ‰))) operator for the phase graph. I know this is an old problem, this graph was actually incorrect as seen from the comparison with the correct graph of the function Ļ†1. Why does this happen?

digBode.jpg

1 reply

W
Werner_E25-Diamond I
25-Diamond I
September 18, 2019

The real part of X01 is always negative. So I would expect angles in the range [pi/2; pi] or [-pi/2,-pi[ for the phase.

The atan function never would give you these values (its restricted to [-pi/2; pi/2]). You would have to use atan2.

-
-MFra-21-Topaz IIAuthor
21-Topaz II
September 18, 2019

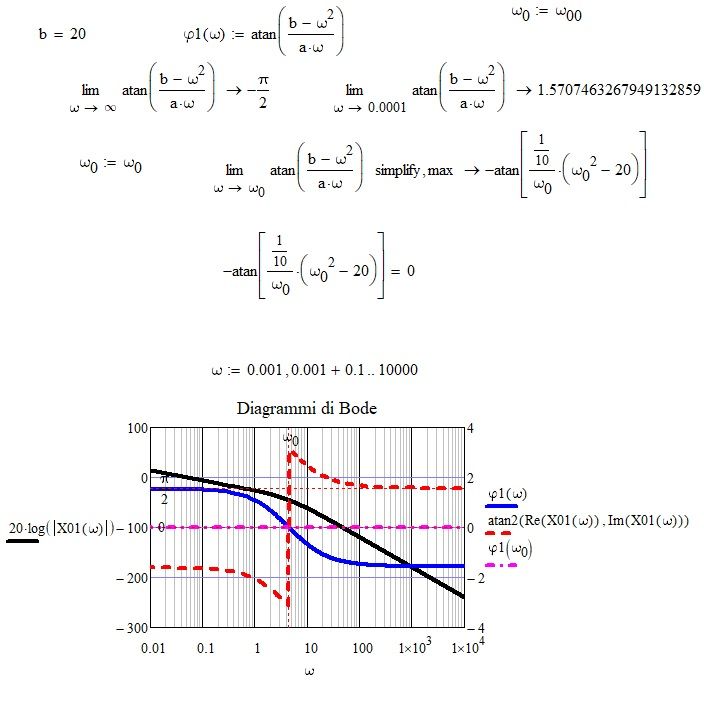
It seems to me that even with atan2, nothing changes:

answer 14.jpg

W
Werner_E25-Diamond I
25-Diamond I
September 18, 2019
@-MFra- wrote:

It seems to me that even with atan2, nothing changes:

 

Correct. This is because both arg and atan2 give you the correct results and I think your phi1 is wrong (phase shifted by pi).

 

When you calculated (symbolically) Im(X1)/Re(X2) the denominator was cancelled and the result was (b-w^2)/(a*w). This was the place where you lost the signs of the real- and imaginary parts. The real part ALWAYS is negtive and so the phase can't be anything in the range (-pi/2; pi).

 

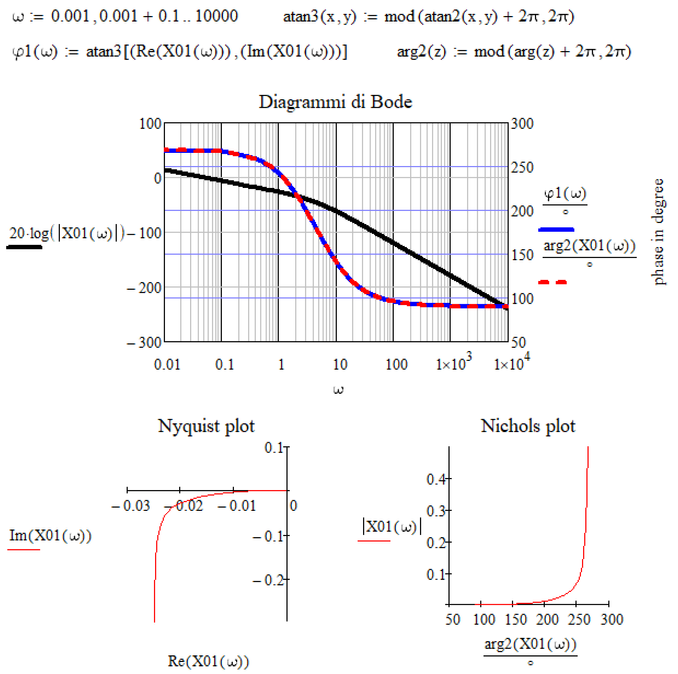
atan2 and also the arg function always return values in the range ]-pi; pi]. This is the reason for the jump when w^2=b at w=4.47 when the phase is +- pi (and not 0!)

You may consider creating your own arg or arctan function which instead always returns values in the range [0; 2pi[ to avoid that jump.

I used the modulo function to do the job but you could as well use an if statement or the if function to achieve the same effect. In case you'd prefer negative phase angles, you would replace the +2 pi by - 2pi.

B.png

Terms & ConditionsCookie settingsAccessibility statement