Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Bug with symbolic solve?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Bug with symbolic solve?
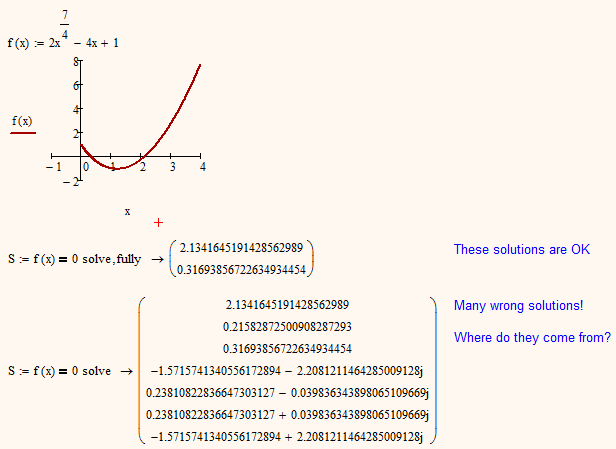
Has anybody an explanation why the symbolic solve produces that many wrong solution if used without the modifer "fully"?
May we call it a bug? Are there other examples?
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think it's clear enough where the extra solutions come from; Mathcad must do something like the following on solving the equation.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
May we call it a bug?
![]() . Is there something else we might call it?
. Is there something else we might call it?
Has anybody an explanation why the symbolic solve produces that many wrong solution if used without the modifer "fully"?
Because there's a bug ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Richard Jackson wrote:
May we call it a bug?
. Is there something else we might call it?
Hmm, its PTC - maybe its a feature!? PTC marketing sure can make that possible.
Has anybody an explanation why the symbolic solve produces that many wrong solution if used without the modifer "fully"?
Because there's a bug
Yes, and obviously "fully" makes the symbolics to think about its results a second time ![]()
Alan's explanation make it clear whats happening - false solutions coming from taking the equation to the power of 4.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
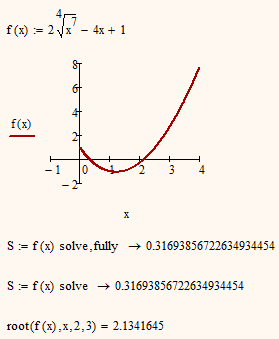
and too few solutions:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
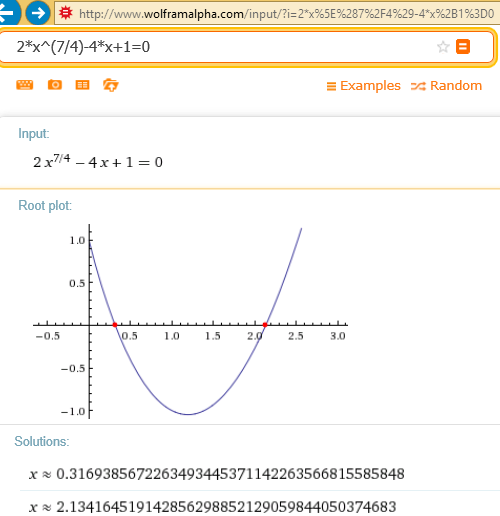
I use others tools in some cases:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Valery Ochkov wrote:
and too few solutions:
Thats indeed interesting and I wouldn't have expected a different behaviour here (because its an even root exponent).
More bugs than I wanted to experience ;-(
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think it's clear enough where the extra solutions come from; Mathcad must do something like the following on solving the equation.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
I think it's clear enough where the extra solutions come from; Mathcad must do something like the following on solving the equation.
Thank! Yes, at least with your explanation its clear what happens.
Nevertheless a bug which should not happen.
Also intersting the different behaviour when using the fourth root instead.
I know the difference between (-1)^(1/3) and the third root of -1 (only the latter is -1) but not sure about the fourth root and how the symbolics sees it.
Werner





