Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Calculate the Theat for a invers quartic potential
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Calculate the Theat for a invers quartic potential
HI friends,
I am looking to get the solution for a Tetha for a quatrics potential from these equations:
(Reference: Classical Mechanics by Herbert Goldstein 1980 2nd ed.)
I have a potential
V(r) = const / r^4.
Can anyone here help me with a MathCAD 15 Sheet, how to do it?
Thanks
Walter
Solved! Go to Solution.
- Labels:
-
Electrical_Engineering
- Tags:
- tetha from potential
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's not completely impossible:
But then there is WolframAlpha:
Now the biggest hurdle may be to have Mathcad calculate the function F, the elliptic integral of the first kind...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Enclosed are functions. Is this what you want?
Cheers
Terry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot, but I need a symbolically solution for that.
I can not do it.
What Could I do?
best
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It's not completely impossible:
But then there is WolframAlpha:
Now the biggest hurdle may be to have Mathcad calculate the function F, the elliptic integral of the first kind...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Best regards
Walter
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have found this sheet for elliptic integrals....but its MMA! Never kind, thanks a lot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You mean 'Mixed Mathematical Arts'?
It's not that bad. In Mathcad 11 its available in the symbolic processor (Maple):
Do you happen to have a set of numerical values for E, l, m and R ?
I might be able to get you a plot of Theta versus r
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Luc,
I have realized that the limits must be chosen carefully to get a real theta angle.
Although the analytical solution is fine, it could be done also numerically.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Certainly, that's possible.
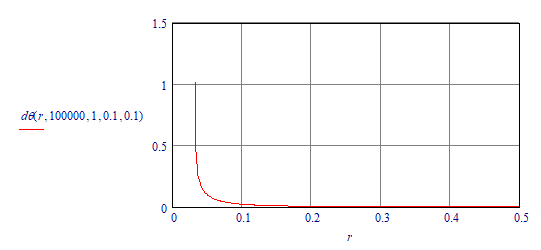
Be careful to choose your parameter values then, and inspect the integrand before the numerical integration. In your case, no wonder you got an imaginary result:
I had to move the values quite substantially to allow r to go/start near 0:
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Awesome! Great! Thanks a lot.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi
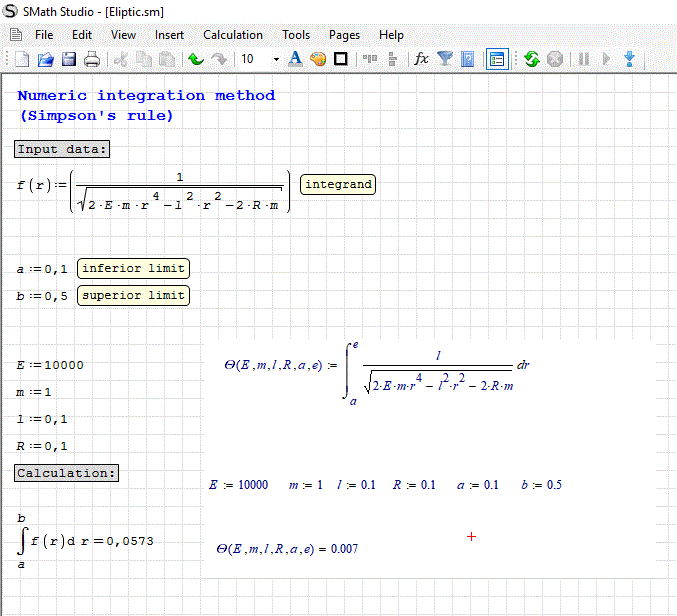
Can anyone here tell me why in teh free SMath Studio there is a other/wrong solution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The upper limit on your inset diagram is e not b. If you change b in SMath to 0.11 you get 0.007 (to three decimal places).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Great!