Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Calculating a derivative of an array
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Calculating a derivative of an array
Hello,
I would like to know if it is possible to calculate a derivative of an array in Mathcad without fitting a function to the data set. A have an expression of a form: sigma(x,y):=A*F,x(x,y), where A is a constant, and F(x,y) is a function of x and y which is defined with a data set/array (data imported from Finite Element Analysis). I would like to calculate a derivative of F(x,y) with respect to x.
Best regards
Rafal
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
- Tags:
- arrays
- data
- derivative
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Rafal,
You should create a program that performs the following operation:
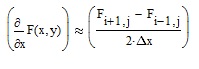
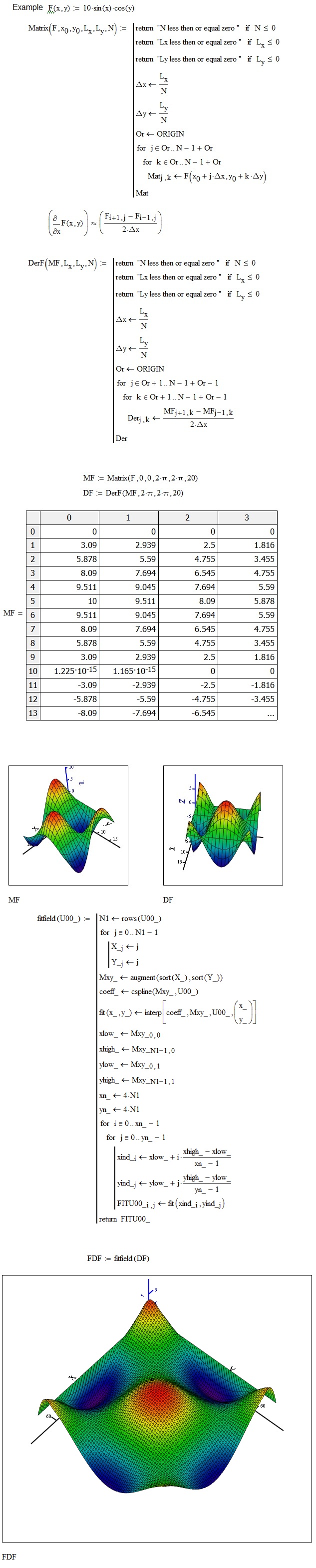
Regards
F. M.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you have a set of discrete points finite difference techniques will give you an approximation of the derivative.
There are fitting functions in Mathcad, numerous options. To get a true derivative you need a function. (I believe.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You are right Fred. Finite difference is one option. When it comes to function fitting, the Mathcad quick sheet "Using Regress: Multivariate Regression" contains a procedure on how to fit a n-dimensional data to a higher order polynomial.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Rafal,
You should create a program that performs the following operation:
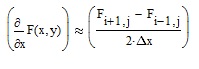

Regards
F. M.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much! This is exactly was I was looking for! It is quite a procedure, very impressive. The program will allow me to calculate a derivative of the solution data imported from FEA.
Best regards
Rafal
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Does this help?


And very simple:

The parabola gives a straight line, the straight line gives a constant.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
Thank you for your reply. Your program indeed works, but it can only deal with a function of one variable F(x). My problem was defined as a function of two variables F(x,y).
F.M. provided a program can deal with a function of two variables, therefore I have selected his answer as the correct one.
Best regards
Rafal





