Community Tip - Did you get an answer that solved your problem? Please mark it as an Accepted Solution so others with the same problem can find the answer easily. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Center of gravity and center of ???
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Center of gravity and center of ???
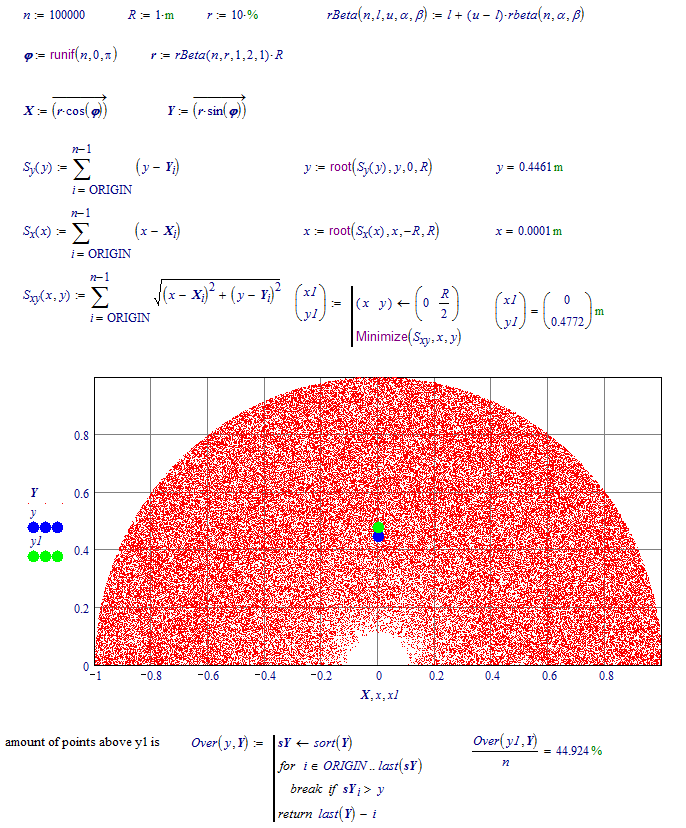
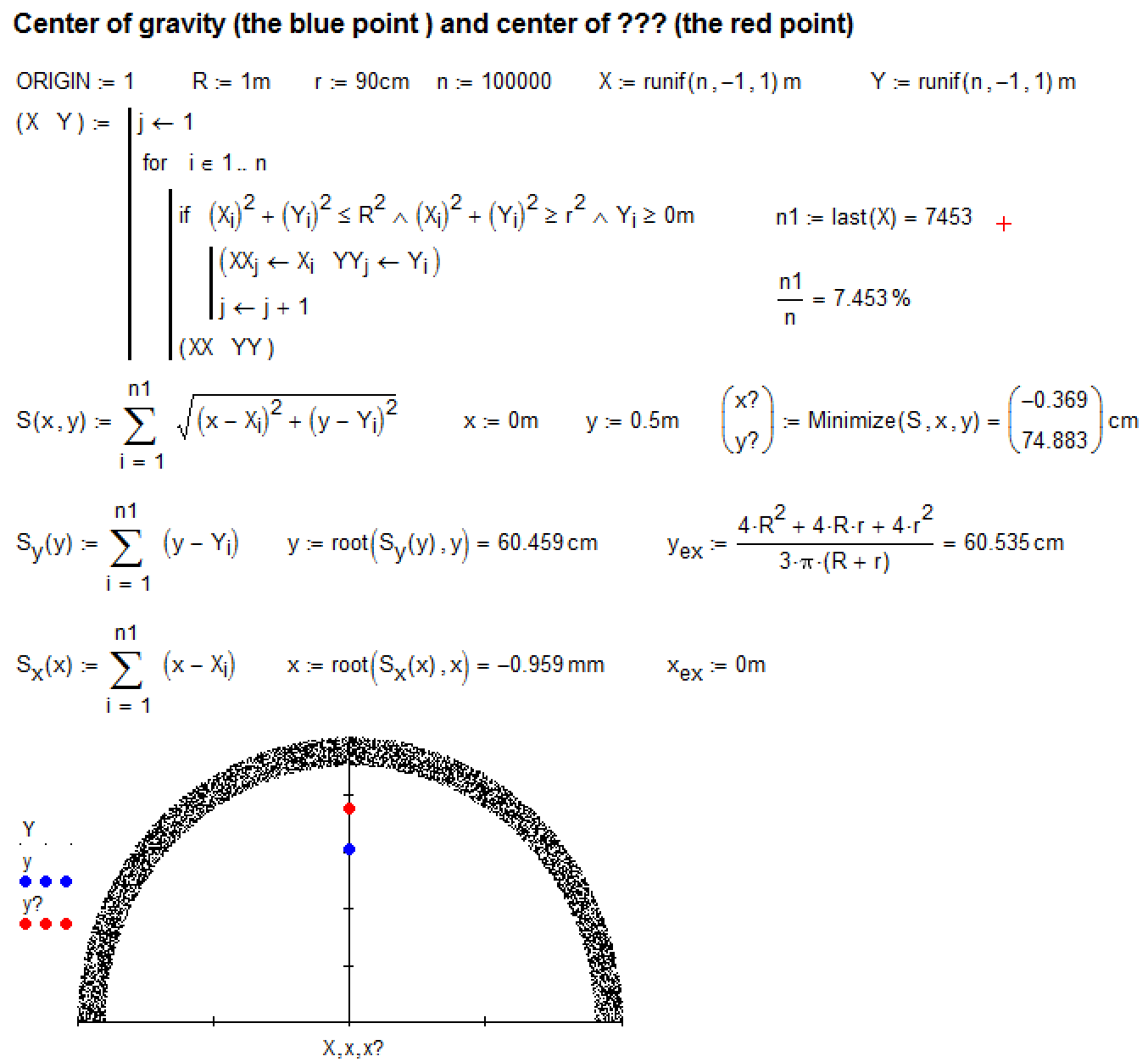
I try to calculate the center of gravity one not simple plane figure.
What is it the red point?
See more please
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Where did you learn that the center of gravity was y = 0.5?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
y:=0.5m was just his guess value for the subsequent Minimize function.
We are all in agreement that the center of mass is at y=61cm.
What is the red point? As defined by the equation, it is the point with the shortest distance to the mass. If it has a name, I don't know it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Okay, sorry, didn't read carefully.
But when I do the same thing:

So I don't see where 74.883 came from.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fred,
Your summation should go from i = 0 to n1 (not n1-1); however, this will make a negligible difference. You would want n1-1 if you had defined n1 with the rows() function, but you used last(), so the -1 is not needed.
The difference in the calculations is that Valery took the square root before summing. When I do the same in your worksheet, I get the same 74.883 that Valery got.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So do I!
Why is it wrong? Minimizing X^2 and minimizing X should give the same result, shouldn't it?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That's what I thought at first, but we're not minimizing X or X^2. We're minimizing a sum.
Here's a quick graph:
The points near y=0 are furthest from x=0, so their effect is stronger on S1 than they are on S2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think you're right!
I took histograms of X and Y:
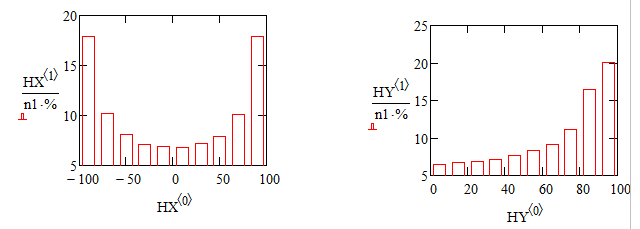
More of the Y's are near the top, while most of the X's are at he ends.
Note that the mean of Y gives the same answer as S2 (aka Sq):
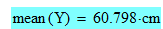

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's a simplified version of the problem worth pondering:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark Gase написал(а):
Here's a simplified version of the problem worth pondering:
One more example
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I find it ever so sad to see that you generate a lot of data, then throw away the largest part of it.
How about:
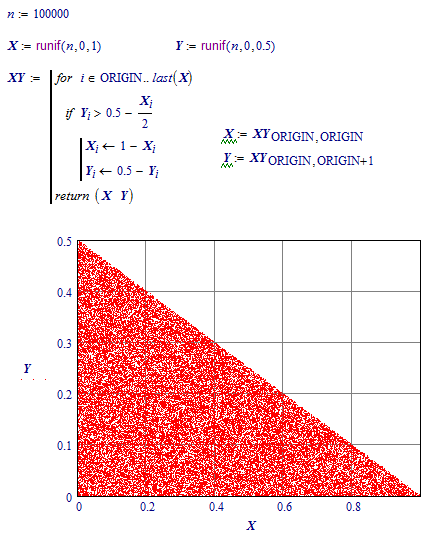
So that you keep your n points.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
LucMeekes написал(а):
I find it ever so sad to see that you generate a lot of data, then throw away the largest part of it.
How about:
So that you keep your n points.
Luc
Sorry, but better to have same density of points in horizontal and vertical dimensions!
Not 0..1 and 0..1/2, but 0..1 and 0..1
And second - Do you red my letter about your address?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Does this help?

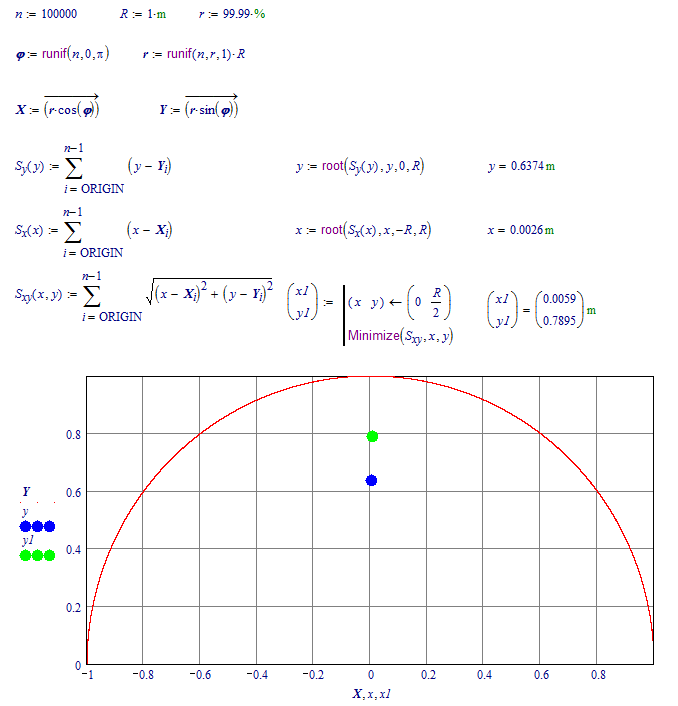

If you change the 'thickness' of the semi-circle, the amount of points with y above y1 doesn't change as much as y1.
Extreme example:
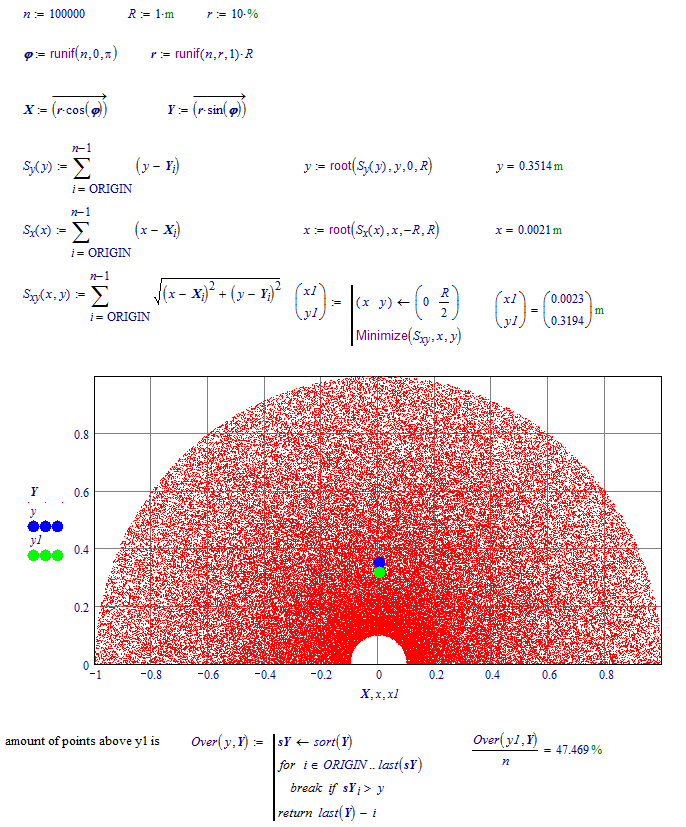
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc,
The way you have defined the data points, there are more near the inside radius than the outside radius. This is especially visible in your last graph.
Valery's setup made the points uniformly distributed throughout the whole area.
This will skew some of your calculations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark,
I agree.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark Gase написал(а):
Luc,
The way you have defined the data points, there are more near the inside radius than the outside radius.
It is not correct but more nice! ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Luc, to get a uniform distribution of points over a circular area you need to generate a uniform distribution for r^2 and then take the square root to get r (as well as generating a uniform distribution for phi, of course).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Ah, sure Alan! Why didn't I think of that. So like this:

Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark Gase написал(а):
The red point is the geometric median.
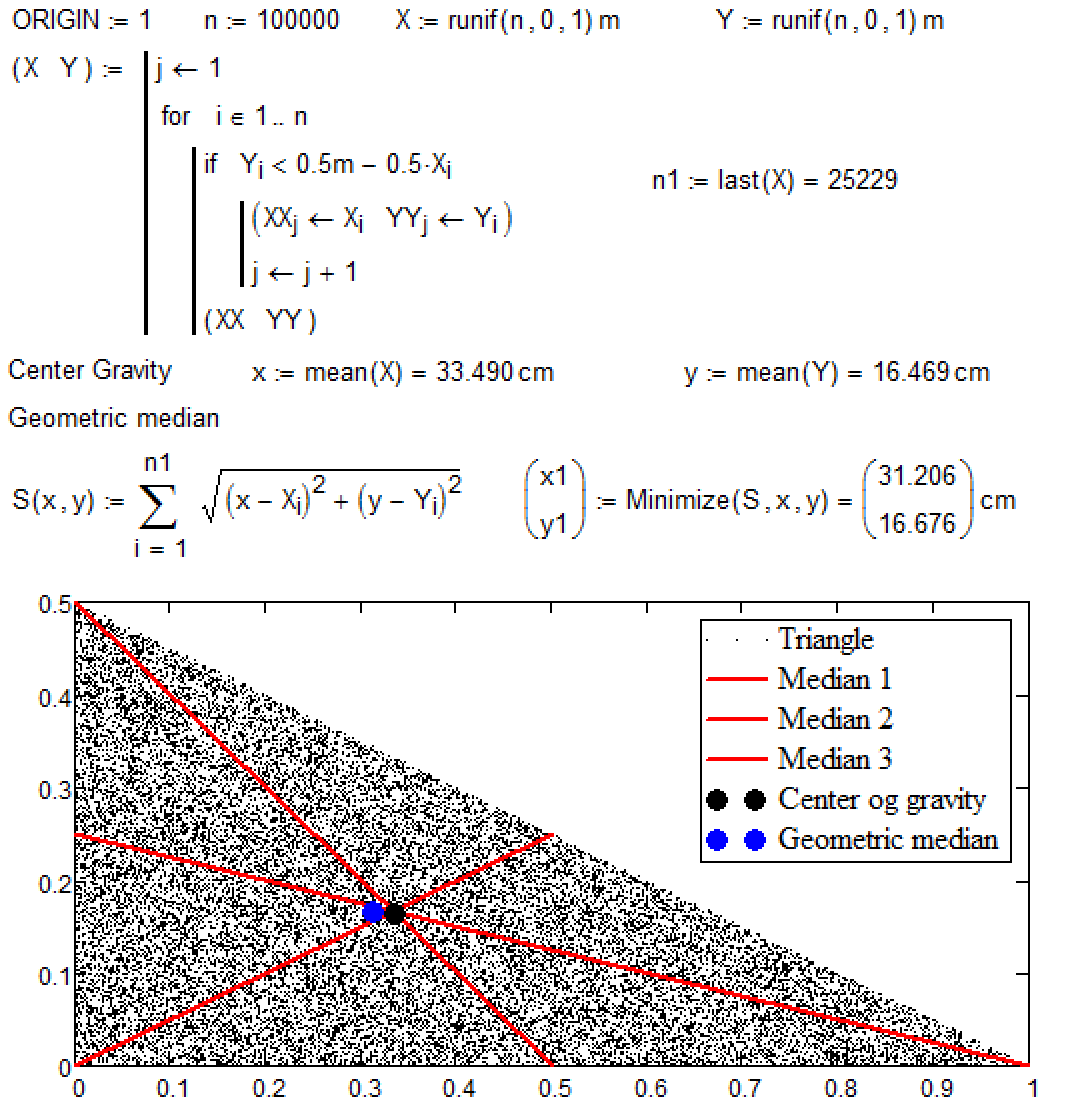
We must check in on one triangle with three medians!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
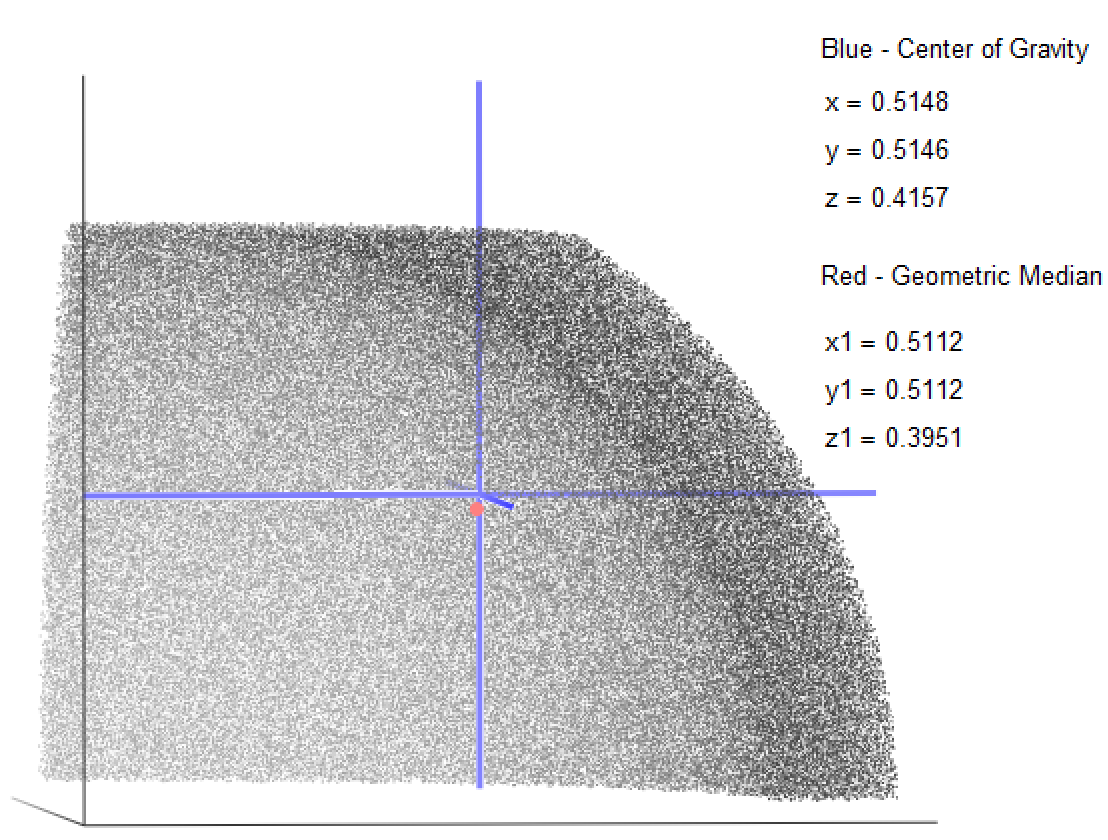
I think the geometric median and the center of gravity must be one point ![]() .
.
Why?
See please two method of the searching this point:
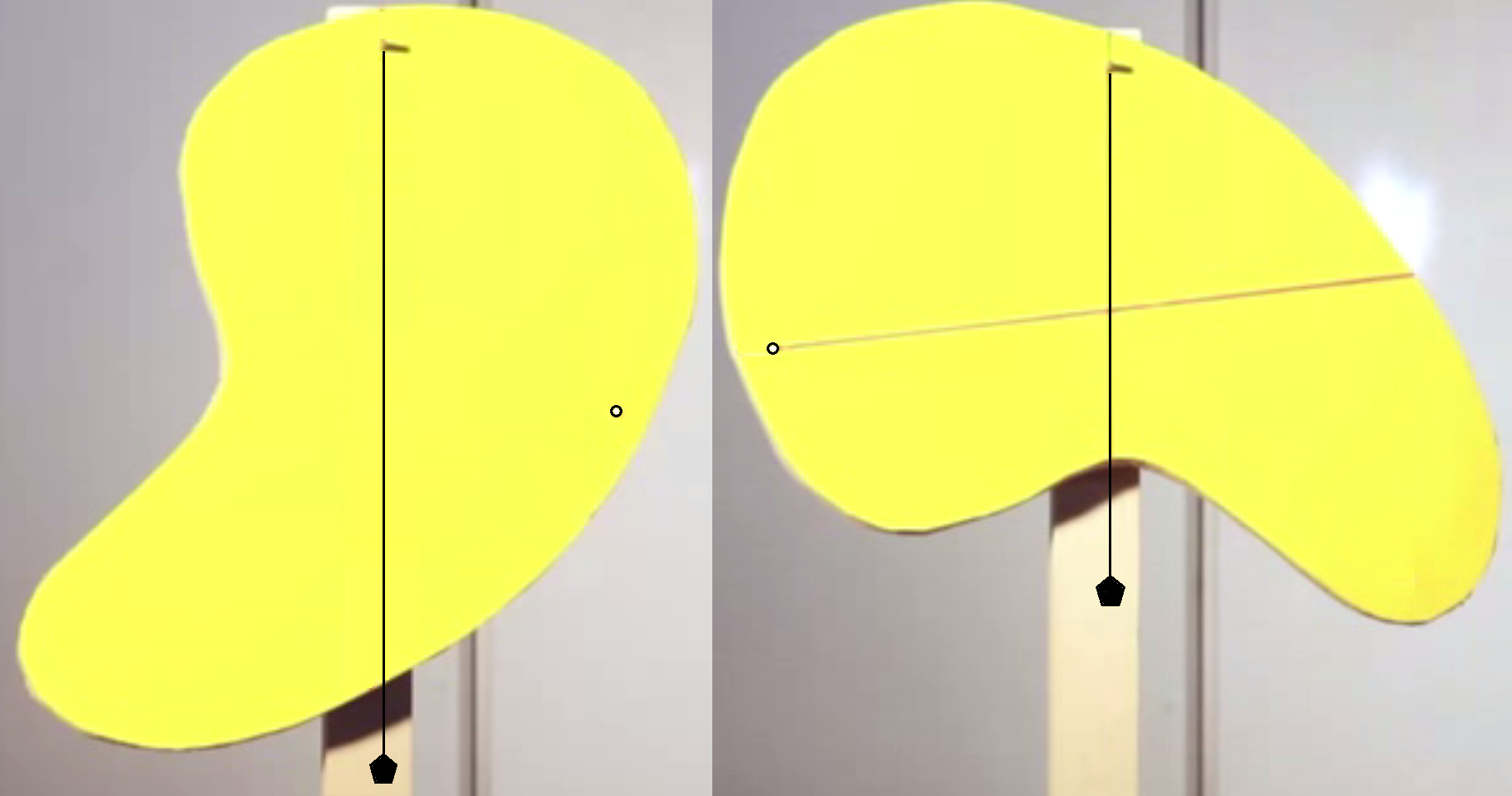

But we have by using our (Monte-Carlo) method;
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry!
This point is
or geometric center.
If our figures have constant density - geometric center = mass center!
Why we have: geometric center and mass center are two different points at constant density?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In geometry, the term "barycenter" is synonymous with centroid, the geometric center of a two-dimensional shape.
That means:
barycenter = centroid = geometric center = center of mass w/ constant density
Valery Ochkov wrote:
Why we have: geometric center and mass center are two different points at constant density?
You have two points because the geometric median is not the same as the geometric center.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mark Gase написал(а):
In geometry, the term "barycenter" is synonymous with centroid, the geometric center of a two-dimensional shape.
That means:
barycenter = centroid = geometric center = center of mass w/ constant density
Valery Ochkov wrote:
Why we have: geometric center and mass center are two different points at constant density?
You have two points because the geometric median is not the same as the geometric center.
Sorry, Mark,
but with constant density the geometric median is the same as the geometric center. Or?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, Mark!
It is the geometric median!
But what is the name this point in German, French, Italian, Russian....
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Two pictures and sheets for thinking!
Three points! Why?

One point!
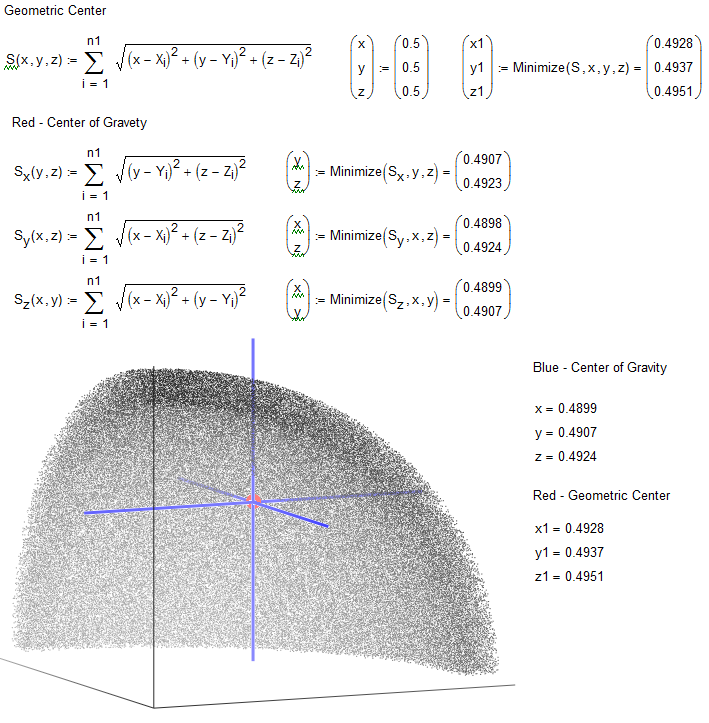
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Center of Gravity... 4D-body
Where is the plot? I want an animated XYZ plot with W as time.