Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Chemeng Problem: Floating Point Error Runge-Kutta 4th order
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Chemeng Problem: Floating Point Error Runge-Kutta 4th order
Hello! I am a newbie to this community ![]() . I would really appreciate any help with my problem.
. I would really appreciate any help with my problem.
First of all, i was asked to apply the Runge-Kutta 4th order method to solve this problem.
I managed to get something out of this, but when i change the value of the rate constant (k), for valutes >2, i get a floating point error.
My aim is to get 9 different k (rate constants), ranging from 1 to 10, in order to get (via the Runge-Kutta) the C values of my components (i have named them x and y) . Then the C-t curves will be compared with my experimental curve.
However, whenever the value of k is greater than 2, i get a floating point error ![]() . Any advice?
. Any advice?
Any suggestions or corrections would really be appreciated.
I attach you the mathcad file:
- Labels:
-
Physics
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You algorithm doesn't seem to converge.
For k:=3 its the iteration step at i=48 which throws the error.
x.48=y.48=5.89*^10^291. Your functions f multiplies x and y and the result would exceed Mathcads limit of approx. 10^307, so you get the error.
You can insert a trace command in your program and toggle debug (menu/tools) to watch the variables in your program.
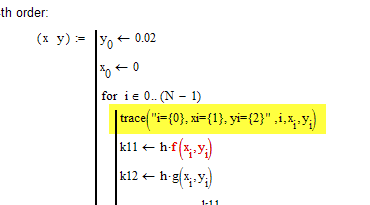

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathematic is not mathematic without animation ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Well guys, thanks for the posts! I found the problem. It was a problem at the mass balances (should have a minus not a plus in front of k). The solutions i had with k=1 and k=2 were unrealistic in a chemical way (CNaOH was valued way greater than it should have been), σο i rechecked the problem.
Thanks for your help Werner! One word (not converge) gave me a serious hint!
Have a nice day!





