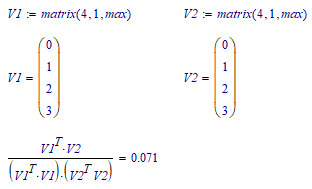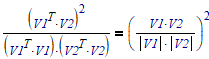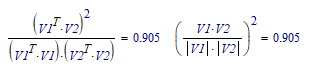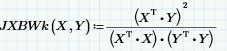Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Comparing two vectors of length N - fundamental math question
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Comparing two vectors of length N - fundamental math question
To all
Not really a Mathcad specific question but a “fundamental “ math question. I know that some of the regular contributors to this forum have the expertise.
I am comparing 2 vectors {v1} and {v2} of length N using the formula
[{v1}T*{v2}]^2 / [{v1}T{v1}*{v2}T{v2}]
where T = Transpose
I did a check using 2 very simple vectors of length 11 so that for x = [0,1..10]
V1 = x^2 and v2 = 10*x
Using the formula I get 0.938 thus suggesting that these 2 vectors are very similar. But clearly they are not!
Has anyone got “insight” on this? It’s quite common to use this formula in some engineering field and setting-up a threshold of > 0.9 as acceptable to assume that the vectors are similar. in this case this is telling me that a stragith line is almost as good as a parabola.
Thanks
Regards
a link: here
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I have my doubts. I created two equal vectors and did the test:
Would this indicate they're not even nearly equal?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My apologies I mis-typed the equation. It should read [{v1}T*{v2}]^2 / [{v1}T{v1}*{v2}T{v2}]
I'll correct the orignal post
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I still have my doubts, but I suggest an alternative, which is simpler:
Got the idea from: https://math.stackexchange.com/questions/1277288/what-is-the-best-way-to-see-if-vectors-are-equal
Where it says:
"You could compute the dot product of the two vectors, and if they are parallel (same direction) their dot product will be equal to the product of their individual norms."
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
with "1/(rows(X)-1)" i get values outside of [-1...1]; try with a small vector. Guess it must be 1/rows(X) maybe?
Note that in mathcad (11, 15) 'stdev' is the variance over all n elements (rather than n-1). The "1/(rows(X)-1)" works with Stdev(), not with stdev()...
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks but don't think so. The MAC for eigenvectors (remember your helicopter days!)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes : why (v1Tv2)(v1Tv2) at the denominator and not [{v1}T{v1}*{v2}T{v2}] ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Error, sorry.
Correction:
Now it makes sense.Especially since it appears that:
e.g. for the random vectors:
Or in general (for real-valued vector elements):
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No need to apologies – easy to make mistake with such things. I couldn’t re-type the equation correctly in the 1st place !
So back to the “fundamental” question – I know it’s not quite the forum - maybe I ought to ask a “pure” math forum?
Would you agree that if you were to compare the 2 (eigen)vectors V1 = x^2 and v2 = 10*x one gets something like 0.93 which is telling us that these 2 vectors are very “similar” (if we accept >0.9 as acceptable). I find this rather mis-leading
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Pearson's r:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Found another source, on Wikipedia: https://en.wikipedia.org/wiki/Cosine_similarity
Basically it suggests a formula that is the same as my proposal, which means taking the square root of your formula (and omitting the sign...).
Success!
Luc