Hi everyone!
It seems strange to me, but I am not finding in the forum any previous post to the subject. I need to calculate the Complete Elliptic Integral of the 2nd kind.
Since it will be evaluated many times inside a double loop, it would be probably unwise to define it using its "integral definition", because of performance.
(from Wikipedia... sorry, I am not a mathematician...)
Has someone good advice for me? What I am going to try is to use the "Gauss hypergeometric function" that seems to be available in Mathcad (fhyper)
Nevertheless I am unsure if this is a good idea.
Thanks a lot for any hints
Best regards
Claudio
ACCEPTED SOLUTION
Accepted Solutions
Hi Stuart and thanks!
yes I believe this is the way I decided to go! Although I programmed it with inverted signs (due to Wikipedia): That means the first argument is -1/2, the second 1/2.
I made a short test and the results seems to be identical. Thanks a lot, apparently this is the "way" to compute the elliptical integral in Mathcad.
Have a nice day
Claudio
Claudio Pedrazzi wrote:
Hi Stuart and thanks!
yes I believe this is the way I decided to go! Although I programmed it with inverted signs (due to Wikipedia): That means the first argument is -1/2, the second 1/2.
I made a short test and the results seems to be identical. Thanks a lot, apparently this is the "way" to compute the elliptical integral in Mathcad.
Have a nice day
Claudio
I'm having second thoughts about the hypergeometric function implementation. (Well, when I say "thoughts", I mean the random firing of the miswired neurons that pass for my brain)
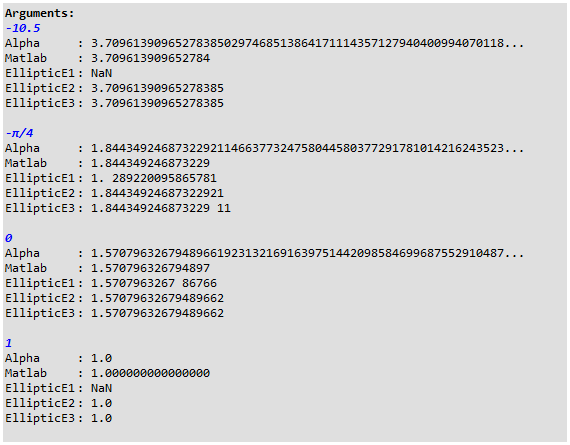
One of these random thoughts made me wonder how the values and execution times might differ between the different means of evaluating the elliptic integral. So I created an integral representation, looked up some values in Abramowitz and Stegun (A&S), and ran a few values in Matlab and Wolfram Alpha. I wish I hadn't because the hypergeometric form is different to the integral values, the A&S values and those of Matlab and Wolfram Alpha ... markedly so.
Unfortunately, the symbolic processor doesn't know about fhyper, so I couldn't it to check that the more limited precision of the numerical processor wasn't the source of the discrepancies. I used hypergeom to get some symbollically-generated values to get round this problem, but (I can't decide whether it's for better or worse), I got the roughly the same values using hypergeom as I did using fhyper.
In addition, the fhyper-based function also had problems evaluating some values (see Matlab / Wolfram Alpha comparison below).
I don't know what's going on, and I haven't had time to look into it in any detail.
Definitions:
Comparisons with A&S:
Comparison with Matlab and Wolfram Alpha:
Symbolic Processor hypergeom implementation:
SymE4, in the results below, is the result of running EllipticE4 on the (0,5..45) degree range
Stuart
well the random neurons produce interesting side effects!
so Stuart, thanks a lot... I am a poor mechanical engineer with interesting fracture mechanics problem some time coming to me ... Although I admire your test, at the moment unfortunately I have no time to make further exploration and will proceed with the hypergeometric definition. But I have to admit that even for an engineer the difference in the third significant digit begins to feel unconfortable .
If you keep the community informed posting here I will appreciate this a lot, whenever you will discover "what's going on".
Thanks for sharing your help!
Regards
Claudio
Claudio Pedrazzi wrote:
well the random neurons produce interesting side effects!
so Stuart, thanks a lot... I am a poor mechanical engineer with interesting fracture mechanics problem some time coming to me ... Although I admire your test, at the moment unfortunately I have no time to make further exploration and will proceed with the hypergeometric definition. But I have to admit that even for an engineer the difference in the third significant digit begins to feel unconfortable .
If you keep the community informed posting here I will appreciate this a lot, whenever you will discover "what's going on".
Thanks for sharing your help!
Regards
Claudio
Problem (partially) solved. Because mathematicians are so fond of rigour and removing ambiguity(ha ha!), there are two definitions of the elliptic integrals in common use. One uses the parameter k, and the other uses the parameter m = k2. The solution is to know which of these two arguments you are dealing with in your problem and then ensure that the elliptic integral also uses that form. Mathematica and Matlab use m, whereas the hypergeometric version I gave uses k. Simply changing x2 to x in the definition gives agreement. The fhyper version still has problems outside of the range 0 to 1, but the other versions seem to be able to handle those. I've added the Matlab ellipticE values for the range 0 to 45 degrees to the check matrix.
I'll have a look at Abramowitz and Stegun tonight ... if I remember.
Stuart
