Curve fitting using a numerically-solved equation

[chuang-4]

Dear all,

I attach here a numerically-solved equation code for you. The tuning parameter in the code is alpha (alpha:=2.4/1.764). What I usually did for my work is to choose different alpha values and to generate the data of gdc vs. t/t_1618. I compare the generated curve to my experimental data and I justify the correct alpha values by naked eyes. Is it possible to modify my code to import the experimental data and let the Mathcad find the alpha value from a least-square fitting?

I really have no idea how I should do that. Could anyone give me some help please?

With best regards,

Chien-Lung Huang

[Fred_Kohlhepp]

I can't find any data in your file, and I'm having trouble seeing what function you're trying to fit.

Mathcad has a wide selection of curve-fitting functions, the Help menu is a great place to start.

[RichardJ]

What you want is possible (not even that difficult, in fact), but we need the data.

[chuang-4]

Please take the following data to fit.

t/t1618    gdc

0.027470231878003    -6.5181281618887

0.0398788385209944    -6.5181281618887

0.0783580530603719    -6.5181281618887

0.101796532274911    -6.5181281618887

0.144411949028619    -6.5181281618887

0.18025903488615    -6.45938729623384

0.215980781282641    -6.25379426644182

0.251827867140171    -5.90134907251265

0.290307081679549    -5.28456998313659

0.32615416753708    -4.67046093310849

0.36187591393357    -3.84808881394042

0.407248798830165    -2.82279370432828

0.433444746187591    -2.11790331646993

0.476060162941299    -1.15134907251265

0.514664716941717    -0.182124789207421

0.550386463338208    0.637577290612702

0.595759348234803    1.75098369870714

0.638500104449551    2.6614671163575

0.683872989346146    3.62802136031478

0.736139544599958    4.80283867341203

0.778880300814707    5.56379988757729

0.81184457906831    6.26869027543564

0.854585335283058    7.08839235525576

0.897200752036766    7.85202360876897

0.942573636933361    8.61298482293423

0.978420722790892    9.22976391231028

0.987946521829956    9.28850477796515

As you could see from the plot in the attached code, very close to t/t_1618 gdc turns down rapidly. You could ignore the fit to this region. Thank you for the prompt help.

WIth best regards,

Chien-Lung Huang

[VladimirN]

Please find in attachment some model that describe your experimental data. To find the coefficients of the equation, I used the built-in function "genfit()".

[chuang-4]

Dear VladimirN,

thank you for the code. The data I showed has its physical meaning and can be described by the original code I posted (it is about a superconducting transition). Therefore by taking any other equations does not help me.

[RichardJ · Accepted solution]

Well, that was more trouble than I expected. There are some numerical issues that had to be dealt with, and when I was almost done Mathcad crashed during a file save, and wiped out everything (the zero byte file problem) . Here it is though.

[chuang-4]

Dear Richard,

thanks so much!! It works. As long as I get alpha it is fine. May I beg for your final help please? What I actually want is to fit t he following data

t/t_1618    gdc

0.04258    -5.63998

0.05434    -5.43703

0.0661    -5.52605

0.07821    -5.25667

0.09021    -5.00185

0.10215    -4.80669

0.11409    -4.65247

0.12612    -4.57127

0.13811    -4.41608

0.15017    -4.2707

0.16207    -4.06022

0.17404    -3.92276

0.18614    -3.91392

0.19799    -3.93296

0.21015    -3.91622

0.2222    -3.91587

0.23417    -3.8601

0.24627    -3.84807

0.25833    -3.79903

0.27027    -3.72393

0.28253    -3.63967

0.29409    -3.54985

0.30588    -3.4791

0.3174    -3.3774

0.32954    -3.28608

0.34163    -3.23156

0.35358    -3.08967

0.36556    -3.06112

0.37721    -2.95127

0.38951    -2.78162

0.40139    -2.62354

0.41346    -2.55322

0.42545    -2.37198

0.43732    -2.19802

0.44906    -2.03337

0.46114    -1.93948

0.47338    -1.75582

0.48477    -1.50693

0.49696    -1.34366

0.50905    -1.18098

0.52058    -0.91148

0.53261    -0.7456

0.54454    -0.56769

0.55653    -0.43944

0.56842    -0.18416

0.58057    -0.04832

0.5925    0.09097

0.60394    0.32735

0.61622    0.45083

0.62816    0.8108

0.64013    0.90426

0.65202    1.10586

0.66374    1.27994

0.67597    1.66356

0.68761    1.74346

0.69996    2.12682

0.71174    2.4368

0.72404    2.81044

0.73596    3.08122

0.74784    3.45396

0.75973    3.85134

0.77164    4.21238

0.78362    4.56011

0.79543    4.94428

0.80739    5.31891

0.81934    5.63133

0.83072    5.86837

0.84317    6.19201

0.85519    6.49611

0.86708    6.90128

0.87924    7.14897

0.89083    7.59884

0.90279    7.81639

0.91429    8.07691

0.92668    8.56495

0.93858    8.74171

0.95057    8.90265

by using following cs_i

instead of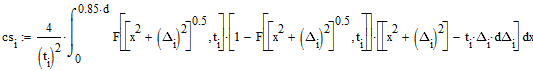

New cs_i is a superposition of cs1_i and cs2_i and beta is a positive number larger than 0 and smaller than 1. cs1_i and cs2_i could have different alpha values. All the other parts in the code are exactly the same. Therefore we have four fitting parameters: alpha1 for cs1_i, alpha2 for cs2_i, 0 <= b <= 1 (in cs1_i), and beta.  Could you do me a favor again to modify your code according to my request please? I guess the fit might have several local minimal values. If you could add somewhere that I could input guess values for each parameters would be much much appreciated. Then I could choose an appropriate set for four fitting parameters.

With best regards,

Chien-Lung Huang

[RichardJ]

I don't want to type those long expressions, so please attach a worksheet that includes them, and the data.

[chuang-4]

Dear Richard,

sorry. Here they are attached. Thanks a lot in advance.

Best,

Chien-Lung

[RichardJ]

When you call the function LeastSqSol the arguments are the guess values for the four parameters.

The double integral is slow to calculate (the numeric integrals are iterative, so it's a nested loop). The double integral is calculated for every iteration of minerr, so it takes a while. Be patient . It's not obvious to me how to speed it up, but I'll think about it.

[chuang-4]

Hi Richard,

It is almost perfect!! However, I see that in the parameter space there are indeed many local minima resulting acceptable fittings. Just one final question to you. If I would like to force b = 0.3 and let other three parameters do free fit, is there a simple way to do that? Sorry to bring you so many cumbersome questions. I thank for your help in advance.

Best

[RichardJ]

Just set b=0.3 and remove it from the argument list so that minerr does not change it:

However, beta is now an unrealistic number. That can be fixed by adding constraints to the solve block:

Note the very heavy weighting of the constraints (10^15) to make them hard constraints. Now beta is within the allowed range, but I think the fact that it's being forced to 1 may indicate that 0.3 is not a good value for b.