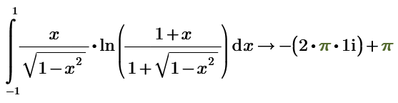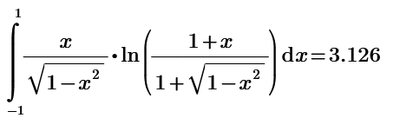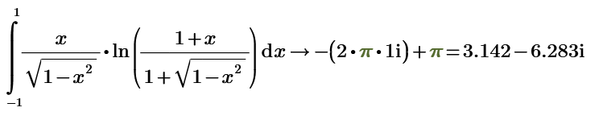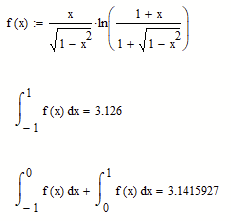Community Tip - New to the community? Learn how to post a question and get help from PTC and industry experts! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Different values when calculating the symbolic and numerical value for the same integral. Is it ok?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Different values when calculating the symbolic and numerical value for the same integral. Is it ok?
Hello,
Why do I have 2 different values when calculating the symbolic and numerical value for the same integral like below example?
Symbolic calculation:
Numeric calculation:
Symbolic calculation first then numeric calculation:
- Labels:
-
Calculus_Derivatives
-
Mathcad Usage
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Did you really expect a finite result?
You may consider opening a support case with PTC support, giving them the opportunity to improve their symbolic engine.
Here are the results with muPad in MC15
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
When I split the integral in two, with limits -1 to 0 and 0 to 1, the numeric result sums to 3.14159269837176, while the symbolic result matches your single integral. The numeric integrator in the Free42 Plus app (an enhanced simulation of the HP-42S calculator) gives 3.14153108100. Both of my numeric results are much closer to pi than yours. I haven't played around much with integrals for several decades and I don't know this particular one at all. Is pi the correct answer?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, it look like the correct result would be pi.
The numeric result of Mathcad can also be improved if the integral is split
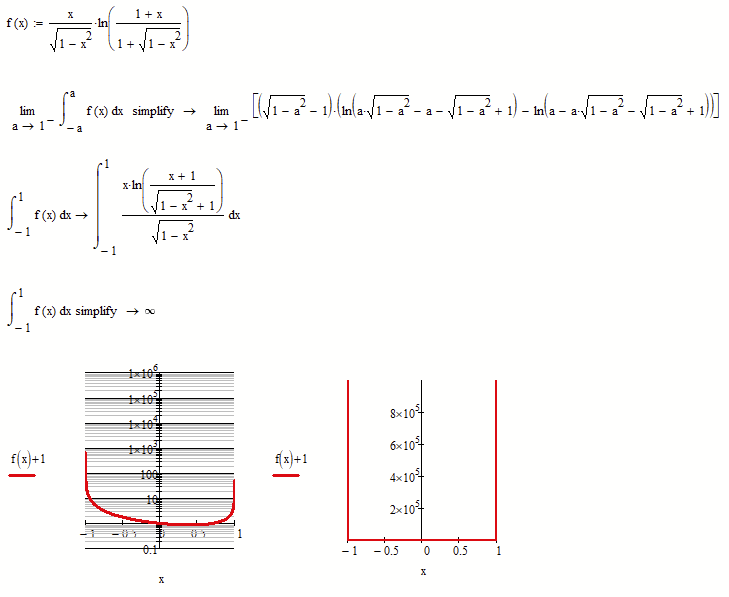
Normally you also can improve the numeric result of a definite integral by decreasing the value of the system variable TOL. But if we set it lower than 10^-7 the algorithm fails ("calculation not converging") because the funcion simply is not defined at the end values +-1. So the correct way to calculate the integral is with variable limits +-a and lim a->1. Unfortunately the symbolics in Mathcad is not capable enough to come up with a meaningful result.
Also Uncle Wolfram does not provide a symbolic result, just a numeric one which indeed is quite close to pi
Best result so far possibly by Prime's symbolics -> pi*(1-2i)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
A 4-piece integral with the limits -1 to -0.98, -0.98 to 0, 0 to 0.98449, and 0.98449 to 1 produces a sum of 3.14159265358989. So, all but the last two decimal places are correct with respect to pi. I could probably get closer to pi with more trials, but this is enough.
It seems to me that this function's very steep tails gives Mathcad fits, both numerically and symbolically. I suspect that the steep tails and the very large ratio between the tops of the tails and the bottom middle of the curve pushes up against floating point limitations, which is why a 4-piece integral produces a better numerical result than a 2-piece integral, which is in turn better than a 1-piece integral. I wonder if doubling (or more) the numerical precision that Mathcad works with might result in a better 1-piece integral solution.
I don't know enough about the symbolic solver to comment on its behavior.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, π is the correct answer for this intergal, but my question was why symbolic result of this integral is different than numeric result of this integral, like I shown above?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Because the numeric and the symbolic processors are different. They use different methods to find an answer. That was the case with (real) Mathcad, and is no different for Prime.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Then which calculation should I trust more, the symbolic calculation or the numeric calculation, if the 2 results are different? When I should rely more on symbolic calculation and when I should rely more on numeric calculation?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You should always be cautious with results from any program. Wherever possible check the results.
Be aware that the numeric processor often gives approximations. Even for simple problems like division 20/6 the result: 3.33333333333 is an approximation of 10/3.
Success!
Luc