1-Visitor

Question

Differentiation of a discontinuous, piecewise function

Forum|Forum|9 years ago
October 10, 2016
5 replies
4426 views

Dear all,

Is it possible to differentiate a discontinuous (sawtooth-like), piecewise defined function (displacement vs. time) twice so that I get an acceleration curve without spikes?

This question concerns the more recent Mathcad Prime incarnations (v3/3.1).

This could be a trigger for my boss to acquire a Mathcad license, since I am currently working in SMath (a free Mathcad-like prog). However, things in SMath don't evolve like I want...

I used to work in Mathcad 13-15, where I once performed Laplace transforms for integration of discontinuous functions, but I don't know if this approach also applies for differentiations?

Thanks in advance for any feedback!

Kind regards,

Jan

Other

R

RichardJ

19-Tanzanite

If you have displacement vs time that is discontinuous then you clearly have infinite acceleration. The only kind of math that will not show you that is math that is wrong. The only way to avoid the spikes is either to not plot the differential functions at the discontinuous points, or make the displacement vs time function physically realistic (i.e. no discontinuities).

A

AlvaroDíaz

12-Amethyst

Hi.

The only one piecewise continuous functions that you can use for symbolic calculus is the heaviside step (F + Ctrl G).

The problem is that it's derivative isn't a function, it is a 'distribution'. The symbolic representation for it is Δ(x), but you must to provide your own numeric representation, because there are not only one, actually it is the limit for some succession of functions.

The second derivative of Heaviside step involves Δ(n,x), where n is the derivative degree of Δ, another distribution without an unique numeric funcional representation.

Those both function can be found in the help under "Symbolics and keywords/Symbolic functions".

Best regards.

Alvaro.

J

janclaeys

Author

1-Visitor

‌Thanks Alvaro!

However, I have a displacement function (using Heaviside to isolate a sine-like curve, piecewise defined to add dwell time) and will have to get rid of the vertical sections, as Richard suggests?

I need speed and acceleration curves to define corresponding functions for viscous friction and inertial force.

Jan

A

AlvaroDíaz

12-Amethyst

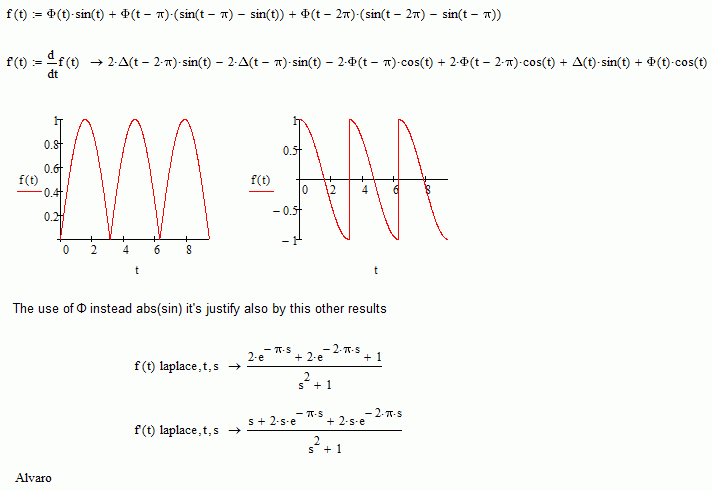
Hi.

This kind of a sine-like function?

Best regards.

Alvaro.

W

Werner_E

25-Diamond I

Is it possible to differentiate a discontinuous (sawtooth-like), piecewise defined function (displacement vs. time) twice so that I get an acceleration curve without spikes?

What exactly are you looking for?

Just plotting the derivatives, a numerical derivative, a symbolic solution? The latter, as was pointed out by Richard, would be incorrect w/o "spikes".

J

janclaeys

Author

1-Visitor

I look for derived functions, will try to add inclined ‌transition curves instead of vertical ones

A

AlvaroDíaz

12-Amethyst

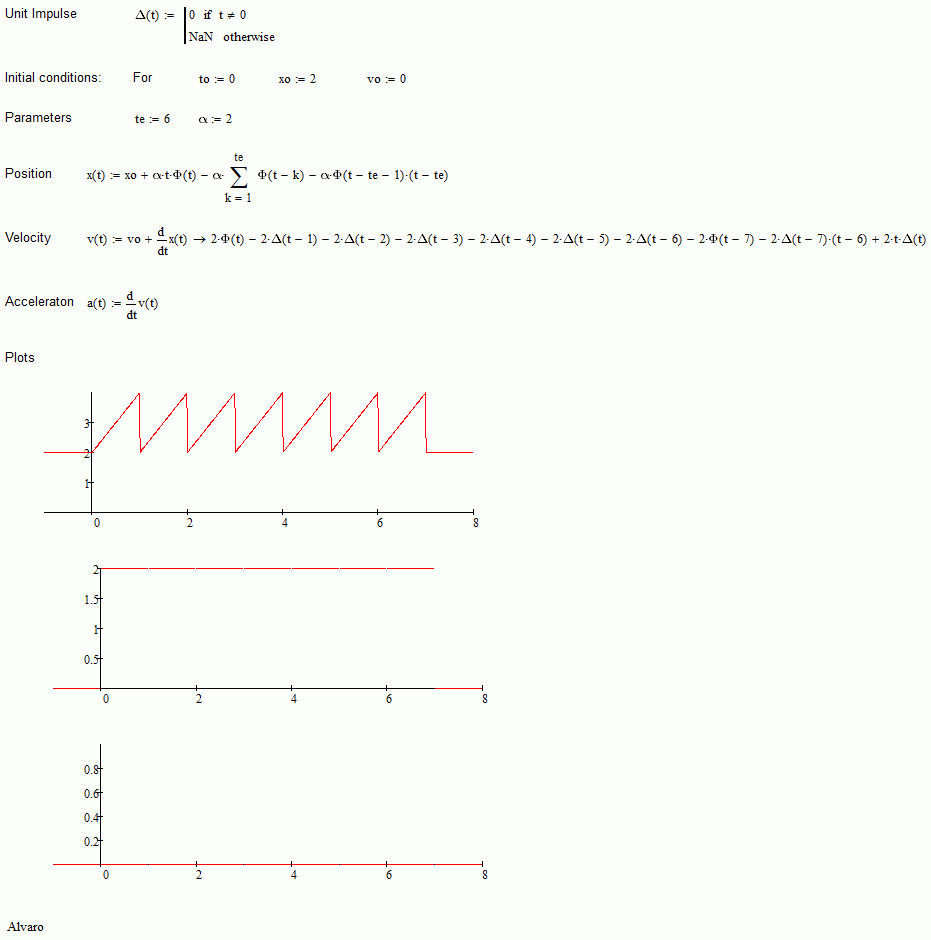
Hi Jan

Attached shows how to use Heaviside step to implement a sawtooth displacement, and get the velocity and acceleration, which actually it's zero.

Best regards.

Alvaro.

1_UnitStep-xmcd.zip

-

-MFra-

21-Topaz II

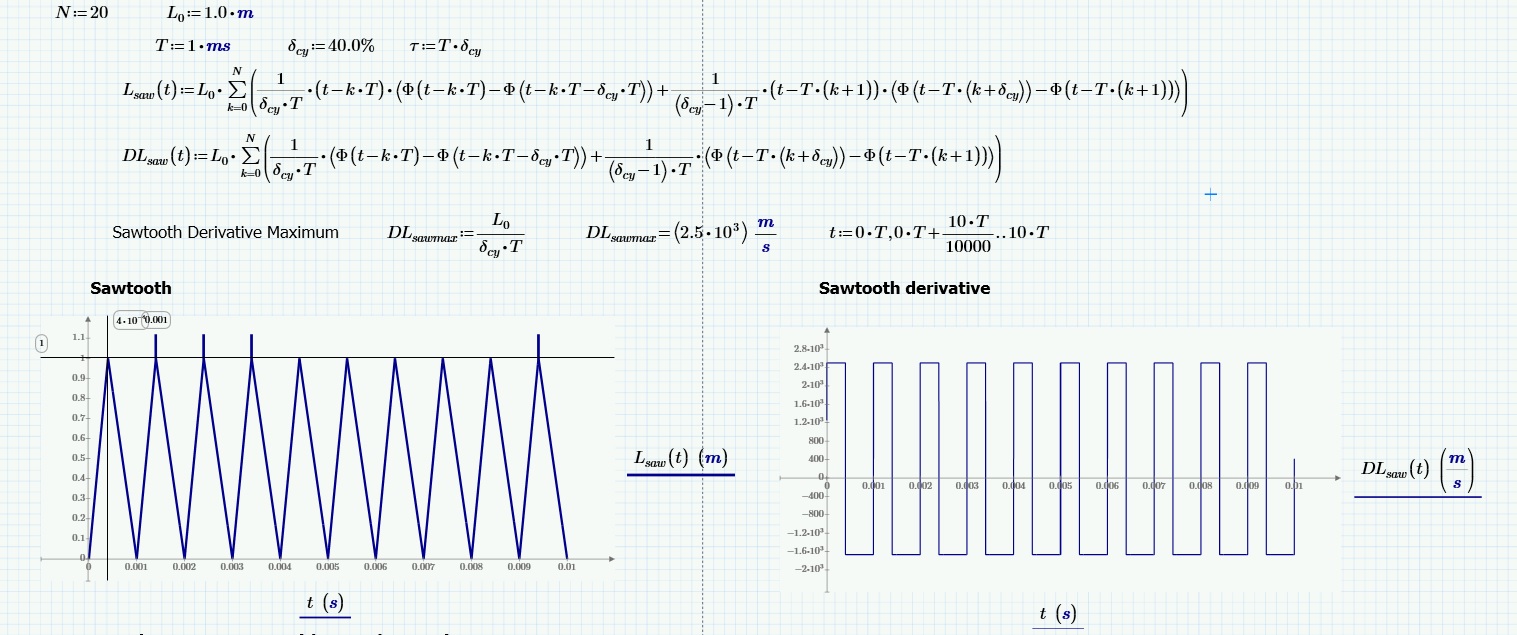
Hi Jan,

What follows is my attempt to solve your problem, but deepening were born other.

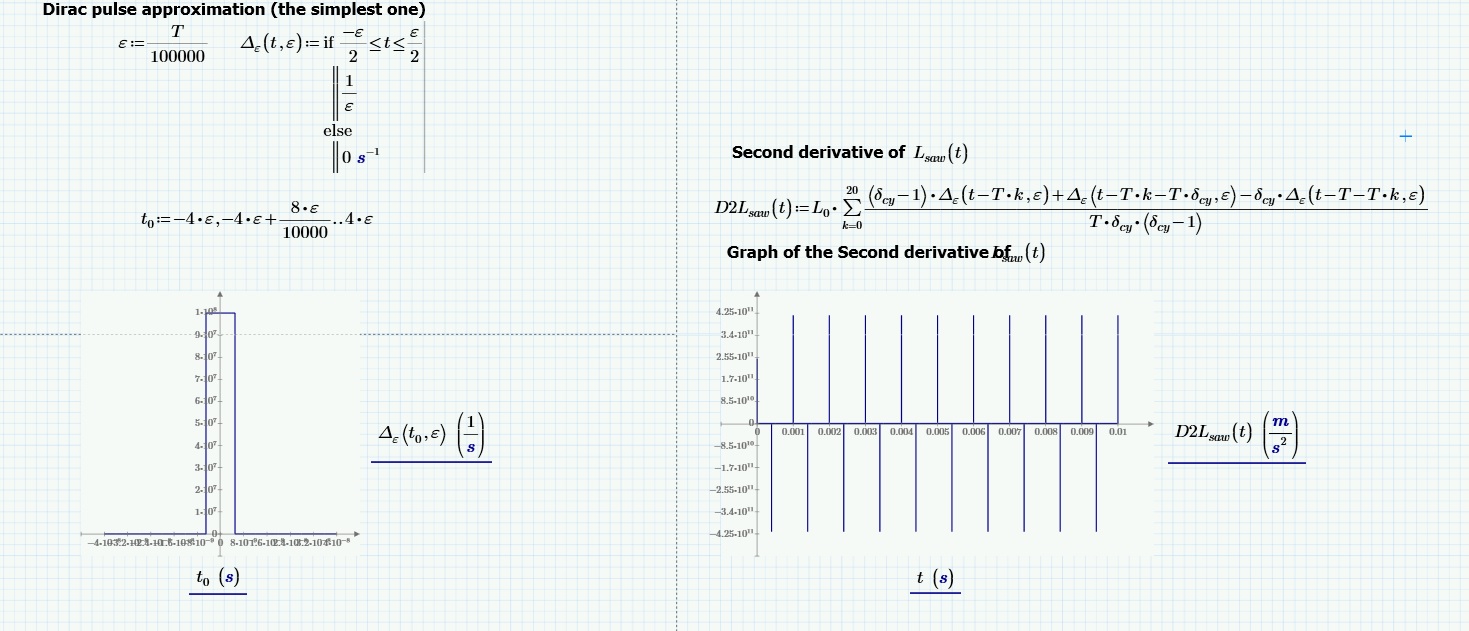
As regards the second derivative, it will be formed by positive Dirac pulses (of unit area, and infinite amplitude) on the rising edges and by negative pulses on the falling edges of the first derivative.

What to do to avoid the spikes?