Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Energy Calculation (heating a decreasing mass)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Energy Calculation (heating a decreasing mass)
There is a good chance I am just being less than intelligent about this but I'm having some trouble calculating the energy required to heat a container of air (a hot air balloon).
In this scenario, the pressure is remaining constant and air just leaves the container as temperature increases and air expands (in other words mass is decreasing).
Since Q=m*ΔT*Cp it should take less energy to heat the decreasing mass then it would to the system if the mass was constant however my calculations are saying otherwise.
I know I'm doing something wrong but I'm just not sure what.
Thanks
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I thick you're getting wrapped around the temperature scale axle! There are degrees Kelvin, and degree Centigrade (which is 273 degrees higher.) Then there are delta degrees Centigrade. One delta C is one delta K, but one deg centigrade is 274 degrees K.
Work in absolute temperature (Which is what Cp wants to see.)
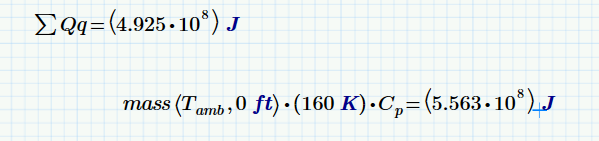
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You've got

then
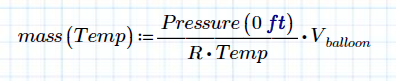
In my Prime 3.0:
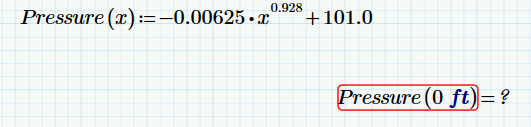
I get an "units don't match" error.
Try this:
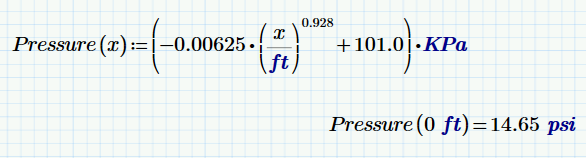
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Haha, thanks, Fred. I actually had that just in the hidden region I felt it was just less "pretty" forcing units into the equation like that. I probably should have shown that in the pdf though sorry about that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I thick you're getting wrapped around the temperature scale axle! There are degrees Kelvin, and degree Centigrade (which is 273 degrees higher.) Then there are delta degrees Centigrade. One delta C is one delta K, but one deg centigrade is 274 degrees K.
Work in absolute temperature (Which is what Cp wants to see.)
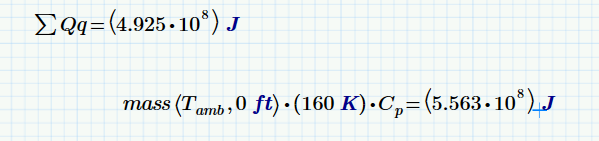
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, Fred! That's a big help. That is a neat trick with iteration. I didn't know you could do that in Mathcad.
To circle back to your point about Celsius and Kelvin is that a mistake I was making or was that a quirk of Mathcad. I ask because I also tried just switching all of my units to Kelvin and I got slightly larger numbers when calculating Joules.
Thanks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Long ago Mathcad had two "built-in" temperature units--Kelvin and Rankine, the two absolute temperature scales; life was simple. But a lot of people complained, wanting to use Centigrade and Fahrenheit scales. For problems where absolute temperatures are required (speed of sound in air for example) using These scales required adjusting the formula to get back to absolutes.
Marketing got enough complaints that Mathcad developed Centigrade and Fahrenheit, functions that do the conversions for us.
Unfortunately, some equations (heat conduction for example) require a temperature difference unit, and the delta Centigrade and delta Fahrenheit functions were introduced.
Now a "newbie" like you comes along with an equation and has to figure out whether he should use delta or "not delta." The result is mass confusion. Figure out each of these:

The "take away" is this: If you don't like your answer, take a hard look at what the temperatures are doing.
I liked the old way!





