Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Equation solving challenge
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Equation solving challenge
Hi everyone, I´m currently working on a particle retention research. I work with mathcad and I´ve reached a point at which solving an equation actually became a challenge that can no longer keep for myself. Said so, I would be really thankful if someone could help me out with this.
Let me explain the situation: I need to find an equation that allows me to match experimental data to the Ho-Zydney model. I´ve tried to do so by working with 4 independent variables which values I must guess, however, doing this takes too much time, as I have to adjust them (or at least try to) one by one. So, I tried to find out a way by using odsolve, but this is not helping me minimize the guess values to those 4 parameters. I´ve been Reading a paper that claims to solve that situation by using Euler´s method and some iterative process, this paper however, does not give much detail about it, so I guess I should stop trying to guess and find another way to solve my problem.
Thank you in advance, I am open to advices related to this particular challenge.
Solved! Go to Solution.
- Labels:
-
Statistics_Analysis
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
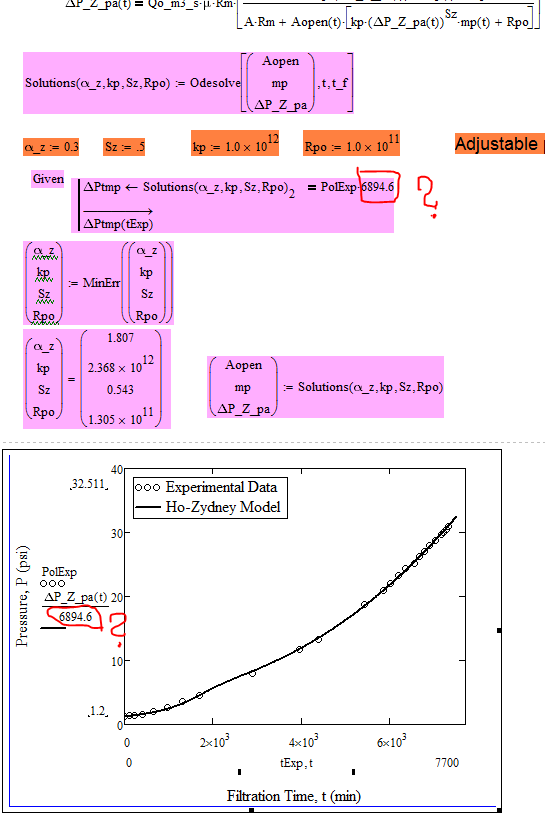
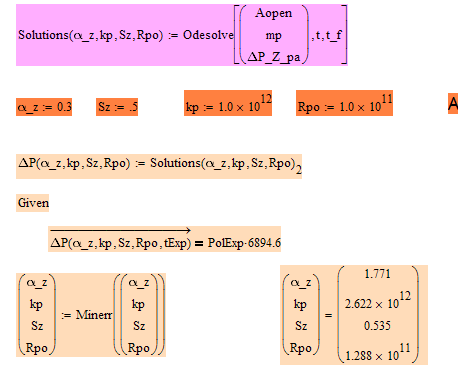
I am not sure what the number 6894.6 should be which you have as scaling in the plot but if its your goal the the two graphs (Experimental data and Ho-Zydney) should be the same, here is a possible solution:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not sure what the number 6894.6 should be which you have as scaling in the plot but if its your goal the the two graphs (Experimental data and Ho-Zydney) should be the same, here is a possible solution:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your time, and obviosly I would like to ask you just one question about your answer, please could you explain me how the second "Given" that you used works?.
Thank you.
PD: the number it is a convertion factor
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your time, and obviosly I would like to ask you just one question about your answer, please could you explain me how the second "Given" that you used works?.
Thank you.
PD: the number it is a convertion factor
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First I turned the ODE solve block into a function of the four adjustable parameters like you did later in your sheet, too.
Then I used a second solve block (the one your question refers to) with "minerr" to play with those parameters until the vector tExp would yield the same results as PolExp when fed into the function DeltaP_Z_pa.
The only constraint in this solve block is a two line function which first calls de ODE-solveblock with the variable parameters, stores the function DeltaP_Z_pa in DeltaPtemp and then calls DeltaPtemp with tExp as argument (vectorized). The result of this procedure we want to be PolExp (times the conversion factor).
Minerr now adjusts the four arguments until the overall error is minimized (you can evaluate the system variable ERR to see how big it is). Minerr by default uses the levenberg-Marquardt algorithm and you can change this by right clicking on "minerr". You may also play with the values of CTOL and TOL to maybe get better precision.
My first approach for this second solve block is shown below. It arrives at the same result but it takes it much more time to do so. the reason is that with this approach the ODE-solve block is not only called in every iteration step of the algorithm (which has to be done anyway) but also for every element in tExp. So its at least 25 times slower than the one I posted.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think you're getting wrapped up in unit conversions.
You specify Pin in Pa, and PolExp in psi, then try to fit a differential equation solution.
Work at sorting out consistent units (and don't forget "UnitsOf()" function)