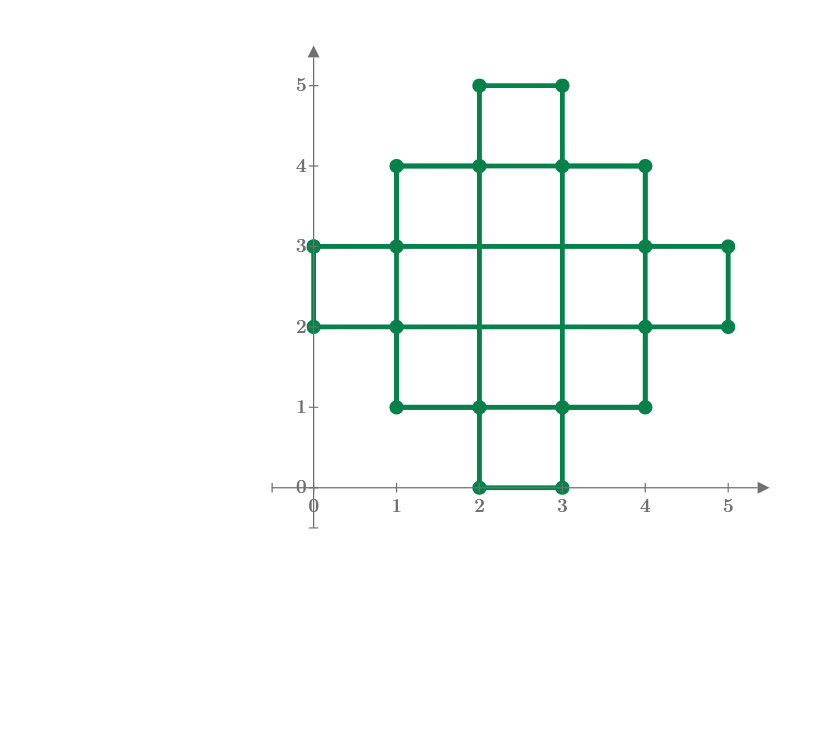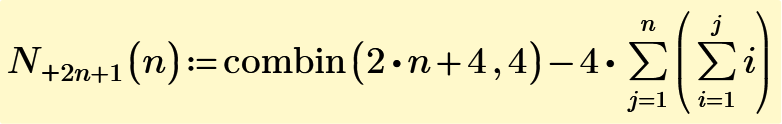- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Find the number of rectangles 2.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Find the number of rectangles 2.
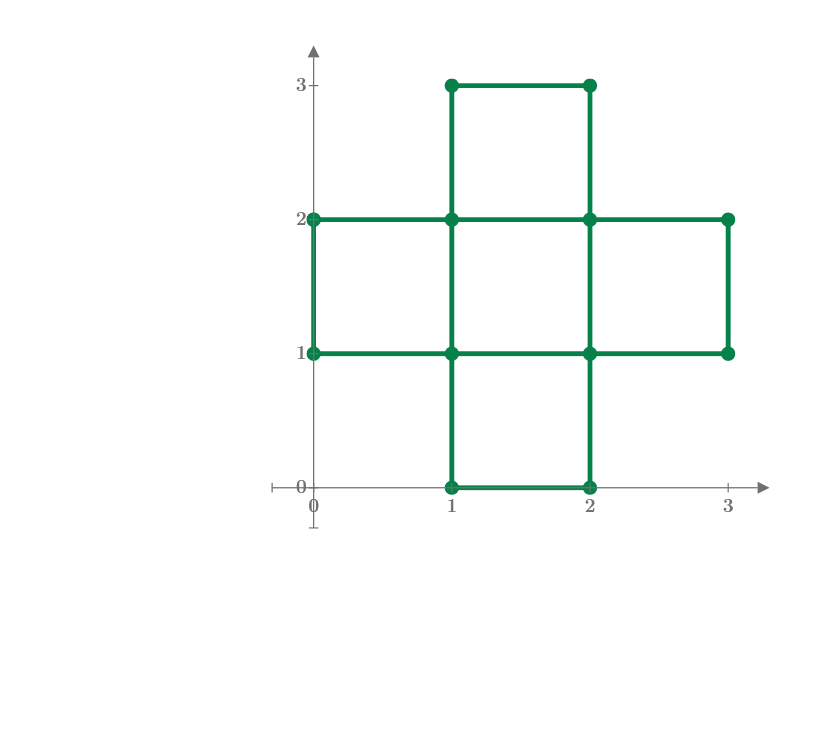
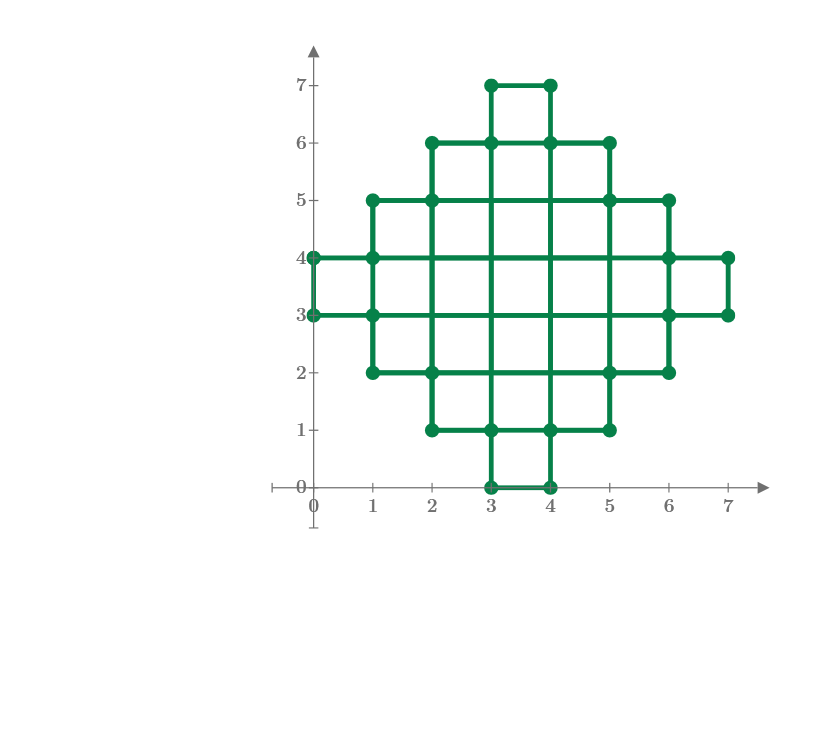
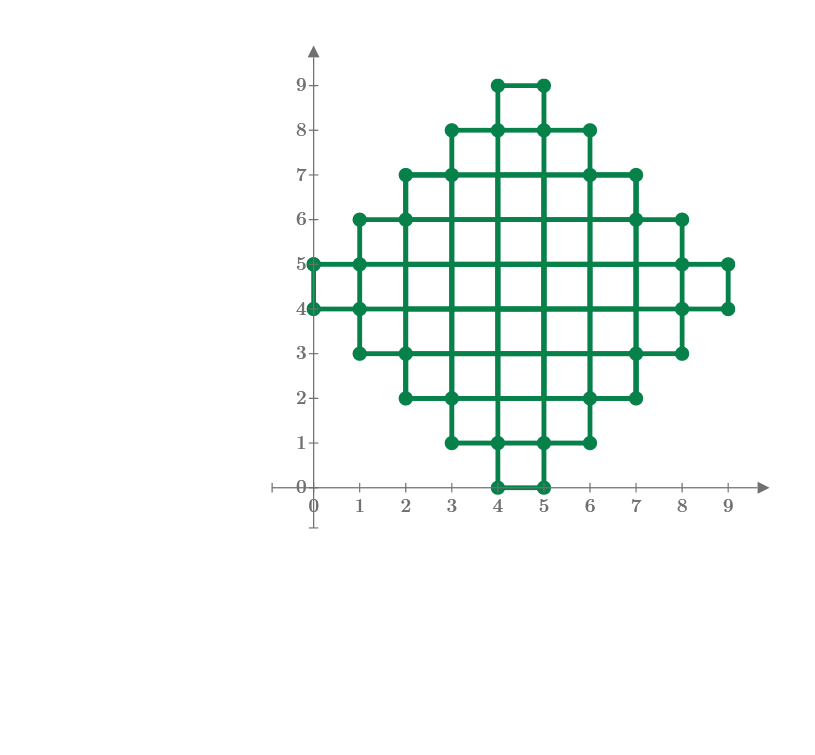
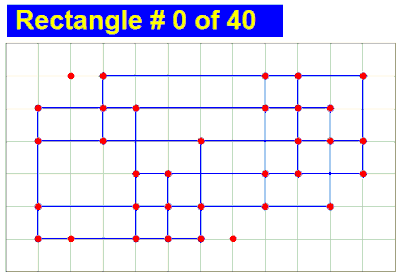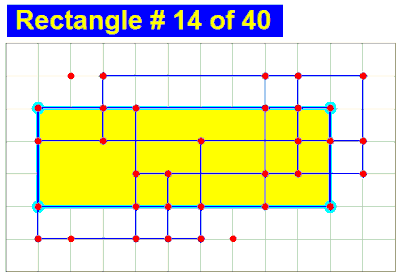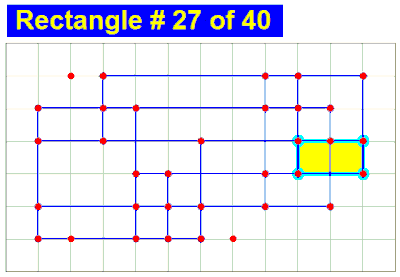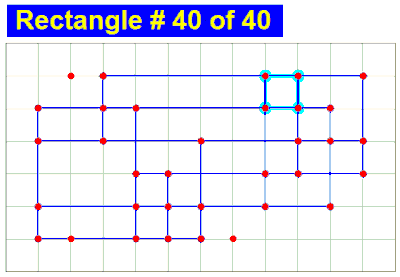
I find very good puzzle from YouTube and show it. Then I made new puzzle to find the number of rectangles of stair-like figures shown here. How to calculate the total number of rectangles included in this figure? I have no formula to calculate this answer, now.
First one, m=3 has 11 rectangles.
Second one, m=5 may have 54 rectangles.
How about m=7 and m=9?
Solved! Go to Solution.
- Labels:
-
Puzzles Games
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
I find very good puzzle from YouTube and show it. Then I made new puzzle to find the number of rectangles of stair-like figures shown here. How to calculate the total number of rectangles included in this figure? I have no formula to calculate this answer, now.
First one, m=3 has 11 rectangles.
Second one, m=5 may have 54 rectangles.
How about m=7 and m=9?
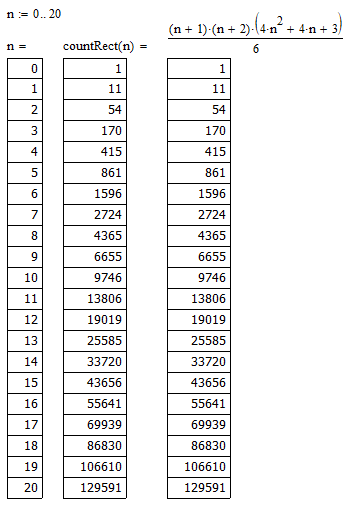
Here you are ( m = 2*n+1)
My function "countRect" works via brute force and could deal with any cloud of points in a grid.
But once you know the first few numbers you can search for the sequence and of course you find it in OEIS: https://oeis.org/A213840
The "n" used in OEIS is "my n" plus one.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ttokoro wrote:
I find very good puzzle from YouTube and show it. Then I made new puzzle to find the number of rectangles of stair-like figures shown here. How to calculate the total number of rectangles included in this figure? I have no formula to calculate this answer, now.
First one, m=3 has 11 rectangles.
Second one, m=5 may have 54 rectangles.
How about m=7 and m=9?
Here you are ( m = 2*n+1)
My function "countRect" works via brute force and could deal with any cloud of points in a grid.
But once you know the first few numbers you can search for the sequence and of course you find it in OEIS: https://oeis.org/A213840
The "n" used in OEIS is "my n" plus one.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here are some animations 😉
Some random points: