Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Finding roots of a graph
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Finding roots of a graph
Hello,
I have plotted the orbit of a satellite using by dericing four ODEs and solving using the rkfixed function. The resulting graph of displacement in the y direction of a cartesian coordinate system is a sine wave.
Is it possible to find the roots of this curve given that there is no initial function? I am trying to determine the period of the sine wave and thus the period of orbit.
I have attached my worksheet. The curve I am trying to find roots for is y(t) in the first graph.
Thanks very much in advance.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
what you call y(t) is in effect not a function but a simple vector. You should call it simply y. The same goes for x, Vx and Vy.
As you are searching the "root" of that "function", essentially you a searching the position of the zeros in vector y and want to know the corresponding values in vector t.
The Mathcad function for this is lookup(0,y,t). The result is a vector with all "roots" but this function would only find an exact match (y has to be exact 0).
Other posibilities would be to use some kind of interpolation or write a routine which looks for a change of sign in y.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you very much guys. They are both very useful responses.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is an appraoch with a small self written routine to find the positions where the sign changes and then uses linear interpolation between the two values.
At the end of the file find a different approach using cubic spline interpolation to turn y in a "real" function (similar to the result of odesolve) on which you could use the standard numeric methods (root, given-find) to get the roots.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If you have a vector (and you do, it's the output of rkfixed) then an fft of that vector will supply the frequency (inverse of period.) What you need is the sampling frequency, the time between data points of the vector.
Look up "CFFT" in help.
Note that Rkadapt, using variable steps, would not be adaptable to this approach.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sounds good, but could you please elaborate on how to calculate the period of y in this specific case of y,t.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Unfortunately not as precise as I'd like, but this is how to do it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks - any reason for setting t.f the tenfold (80k instead of 8k)?
Second question: could the following replace your function dex():
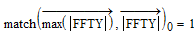
BTW, using the original data t.f=8k and N=1k along with the fact, that the number of points is 1001, we arrive at a period of exactly 8k (instead of ca. 6k).
Any explanation for that big difference? The fft shows clearly, that y is not a pure sine - should this be explanation enough?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Discrete FFT's are by nature approximations. Because you're sampling a cintinuous signal at intervals several things happen:
- If the signal has frequency content higher than half the sampling frequency you will get "aliasing." (Google Nyquist frequency.) For that reason practitioners in real life use low-pass filters to ensure that there are no frequencies high enough to create this problem
- As you can see, the frequency resolution (minimum step that can be resolved) is the sampling frequency divided by the number of samples taken. This causes several issues. First, if the frequency being analyzed isn't an exact integer multiple of the resolution, the FFT will parcel out the energy in the signal between several of the near neighbors. (You can see that in this example.) So, the amplitude of the wave is misrepresented, and the frequency is approximated. (Compare PERIOD with T.)
Your match expression might work for this example. But (for a lot of signals) the zeroth term in the FFT vector is the steady value. (The magnitude of the frequency = 0 term.) In many real life applications, that swamps the varying signal, so I took it out (submatrix(V,1,,,, Further, the second half of the FFT is (for some of the functions in Mathcad) the complex conjugate of the first half, so there are two maximums at least.
At any rate, I'm not an expert, just an engineer who uses FFT's on a regular basis at work. Feel free to improve my technique!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your explanations.
At any rate, I'm not an expert
Neither am I. I'am unexperienced concerning FFT's and the reason I asked was to take the opportunity to learn. While I had to program an fft (real valued) two or three times from scratch, I still don't fully understand whats going on there. In my attempts to follow your advice to use CFFT I came up with that period of 8000 (amongst other, wrong versions) and thought its wrong as of my misunderstanding.
In that file it seems that the value set for t.f is taken as the period (or as a multiple of the period). It reminds at a Fourier series where the interval transformed is always taken as a period of the signal. But I think an FFT is not supposed to do so.
Feel free to improve my technique!
I wish I could but obiously I'm not able to do so.
Anyway, for the original poster in the attached file I provide a third way to get what he demanded. This time using genfit.





