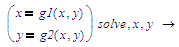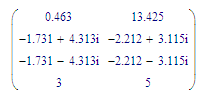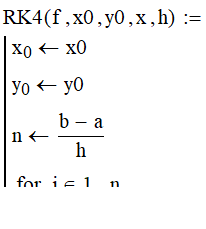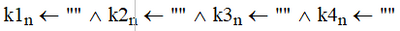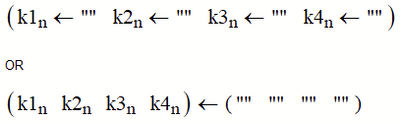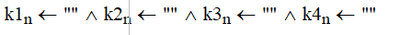Community Tip - You can subscribe to a forum, label or individual post and receive email notifications when someone posts a new topic or reply. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Fixed-Point Iteration for nonlinear systems of equations - my Mathcad alghoritm doesn't work
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Fixed-Point Iteration for nonlinear systems of equations - my Mathcad alghoritm doesn't work
Fixed-Point Iteration for nonlinear systems of equations - my Mathcad alghoritm doesn't work
Hello,
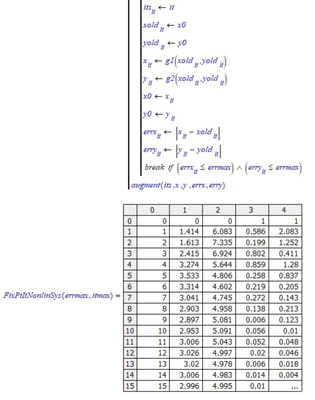
I try to make my Mathcad alghoritm to work for a nonlinear system by using Fixed-Point Iteration . Unfortunately still I cannot get the results. Something is missing in my script. I attached my Mathcad file.
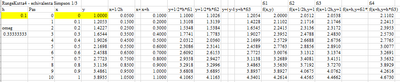
The results whould look finally like this (I obtained it in Excel in order to compare the results if possible):
It xold yold x y errx erry errf10 errf20
-----------------------------------------------
1 2.0000 4.0000 1.4142 6.0828 0.5858 2.0828 0.6023 23.7569
2 1.4142 6.0828 1.6132 7.3348 0.1990 1.2520 3.2299 9.4517
3 1.6132 7.3348 2.4150 6.9238 0.8018 0.4109 4.8888 38.8502
4 2.4150 6.9238 3.2743 5.6438 0.8593 1.2800 1.7585 28.6511
5 3.2743 5.6438 3.5326 4.8065 0.2583 0.8373 1.5000 6.8054
6 3.5326 4.8065 3.3135 4.6017 0.2191 0.2048 1.7316 4.4348
7 3.3135 4.6017 3.0410 4.7449 0.2725 0.1432 0.8185 6.2781
8 3.0410 4.7449 2.9034 4.9577 0.1377 0.2128 0.0356 3.5969
9 2.9034 4.9577 2.8972 5.0811 0.0061 0.1234 0.3272 0.2816
10 2.8972 5.0811 2.9532 5.0907 0.0559 0.0096 0.3124 1.4396
11 2.9532 5.0907 3.0056 5.0425 0.0524 0.0481 0.1223 1.3810
12 3.0056 5.0425 3.0258 4.9968 0.0203 0.0458 0.0363 0.5519
13 3.0258 4.9968 3.0198 4.9785 0.0060 0.0183 0.0852 0.1304
14 3.0198 4.9785 3.0057 4.9828 0.0141 0.0043 0.0574 0.3554
15 3.0057 4.9828 2.9962 4.9947 0.0096 0.0119 0.0121 0.2503
16 2.9962 4.9947 2.9941 5.0030 0.0020 0.0084 0.0149 0.0590
17 2.9941 5.0030 2.9966 5.0050 0.0025 0.0020 0.0184 0.0604
18 2.9966 5.0050 2.9997 5.0030 0.0031 0.0020 0.0093 0.0786
19 2.9997 5.0030 3.0012 5.0004 0.0015 0.0026 0.0001 0.0413
20 3.0012 5.0004 3.0012 4.9990 0.0000 0.0014 0.0042 0.0008
21 3.0012 4.9990 3.0005 4.9990 0.0007 0.0000 0.0036 0.0176
- Labels:
-
Algebra_Geometry
-
Programming
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So your iteration attempts to solve:
That's a set of equations with the following (approximate) solutions:
The problems with your program are due to the fact that the augment() function (of the last statement) needs all its parameters to be vectors.
You have in there x and y, which are vectors (indexed using it), but it, errx and erry are simple scalar variables.
Apparently you want the iteration number, and the progression of error in your table, so you need to make those variables vectors, have them also indexed by it, potentially. Well you shouldn't index it with it, better create a new vector to hold the progressive it values. How about its ?
That gives:
Not quite the result you expected. But at least the error is gone.
Now you find out why nothing is happening after the first iteration.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now you find out why nothing is happening after the first iteration.
o != 0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I was afraid of making that error, and I still did.
But correcting that doesn't help:
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@LucMeekes wrote:
I was afraid of making that error, and I still did.
But correcting that doesn't help:
Luc
Thats strange. When I change just the two o's to zeros in your sheet, the program works as expected:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
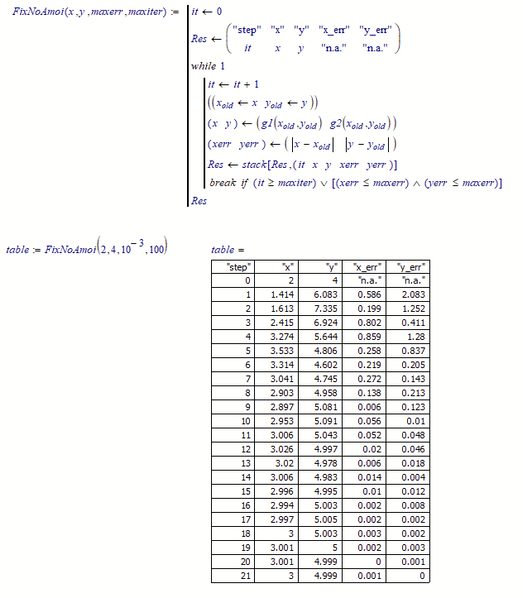
Thanks, in the mean time I solved the block like below. I also attached my file.
- Tags:
- anks
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Good observation. It is more clear on both to put =0.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a slightly different approach
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting the STACK operator.
But "while 1 " understand while.... what ? Who is 1 ? . It performs nicely, but "1" appears a bit with vague status.
The functions f1 and f2 should be kept at beginning because they are the main equations to be solved. g1, g2 are just transformations of f1 , f2.
I will select that strategy that uses "STACK", i like it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Mathcad 1 (or any non-zero value) means "true".
So "while 1" is an infinite, endless loop which is stopped just by the "break" command. I used this way because Mathcad provides no "do ... while" loop and I was too lazy to copy and paste to do the first series of calculations in front of the "while" loop.
You may write something like "while 7=7" to make it clear that its a condition which is always true.
The construction
while 1
...
break if ....
simulates "do ... while ..." or better a "repeat .... until ..."
Not sure what you mean with your comment about f1, f2.
EDIT: Ahh, I see. I was working from the worksheet which Luc had posted (you can see it by the name and the formatting) and obviously he deleted those functions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here is a variant without a break command.
Note that the zero assigned to "near_enough" means "false" and the character before "near_enough" in the while statement is not a minus sign but the logical "non" from the boolean palette.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, indeed, Mathcad as Matlab too, does not support the alternative instruction Do... While.
I am thinking, it is a way to put the algorithm under the function name ?
Just like the table can be put under the variable name:
I want to place the algorithm like this (to save space):
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There's no way to do that.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But its possible to replace multiple repetitive statemets:
with only 1 statement like :
or something else... I attached an example file. I still don't find a more compact way of approach in order to replace that "in column" repetition.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Would the use of 1 x 4 matrices help?
BTW, in the last line in the augment command you should vectorize the function call f(x,y). Otherwise you may get in troubles if your function uses expressions like x*y.
Additionally - the argument x of your function has no effect. You may consider replacing it by the end value of x (=b).
Personally I would prefer to have the number of steps as argument instead of the stepwidth (which may result in an non-integer value for n). Something like
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, the following variant is the best:
I was surprised that "AND" didn't work for "TEXT variables", as for numerical values it accepts serial inputs.
Thanks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How about this? I see no need to delete the last values for the "Ki"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I was surprised that "AND" didn't work for "TEXT variables", as for numerical values it accepts serial inputs.
The explanation is easy. The AND operator (^) is defined for boolean operands only which in Mathcad are simple scalars. 0 means FALSE and every other value means TRUE.
The "result" of an assignment is the assigned value.
K1 <-- 123 is evaluated to 123 which is a valid operand for the AND (^) operator.
K1 <-- "--" is evaluated to the string "--" which is NOT a valid operand for the AND operator and the expression therefore fails.
The same applies to
(a <-- 5) + (b <-- 4) will be OK
(a<--"no") + (b<--"yes") will fail, because the addition is defined only for scalars and matrices, but not for strings
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks. I modified a bit the model of Werner, replacing x_start, x_end that I don't like, but it doesn't show the results correspondingly. I attached.
- Tags:
- modified
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The reason are your first two assignment which again make x and y to vectors. Simply delete the vector index 0 in both assignments.
Your approach makes it necessary that a and b are worksheet variables which have to be defined before the function definition. This limits the use of the function significantly.
You may consider "calculating" a in the program (a <-- x0) .
You present the end value as fourth function argument, but because you named it "x", its immediately overwritten by the very first line in your program.
BTW, you also forgot to put "f(x,y)" in the header under quotes.
So here, no need for any global variables:
I would rather rename the function argument "x" to "b" so the creation of b in the program is obsolete.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
One additional remark:
If you intend to decrease the stepwidth, creating a rather large matrix, you may run into the "eng_exception" error.
You can avoid this by avoiding direct evaluation of the function call. Rather assign the function result to a variable and then evaluate that variable as shown here:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You both are good on this platform. Thank you very much !
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Still exists a small problem. The results are decayed 1 step in the last file Werner shared.
They finally should look like this:
The final solution should be 3.8935 (at step 10) instead of 4.3398 (that is something like step 11, not required). Also, the values k1, k2, k3 and k4 should be decayed about 1 step, maybe. It is also possible to place Res only in last rows of the algorithm, in order to not discontinue the mathematical part ?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You may simply exchange the last two statements in the loop
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Finally I got the trick. You deal with the initial conditions notation in order to obtain an additional STEP inside the loop.
I got also that STACK itself is get building progressively function of the LOOP PROGRESS, That's why you needed an initial form of Res just before the LOOP. Smart !
Otherwise, alternatively to STACK function you had to vectorialize the matrices of iterative results.
Without those tricks the algorithm tends to display only the last iteration results. I worked a lot to change that but finally I got that the ways are those to presented upper.
Indeed, useful tricks.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I had already written it above - the fourth function argument (x) of your RK4 has absolutely no effect as its immediately overwritten by your first program line. You could equally well omit it. The end value is provided by the global variable b.
Personally I prefer functions like RK4 to be self contained - they should get whatever they need via the argument list. Your function still depends on a and b being defined on worksheet level and before the definition of the function. IMHO a big drawback and limitation. Why don't you put at least (a b) <-- (x0 x) as very first line in your program? This would do the job pretty well and it would not be necessary to define anything before the function definition, the program would be self-contained.
You are absolutely right that the header row is necessary to make the subsequent stack commands work. But using vectors for x,y, etc. as in your initial attempt is not the only alternative. We can also use the ability to assign complete columns to a matrix:
MC15 worksheet attached
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now the solution is perfect in 2 variants attached. We also escaped from putting the Tab Header at the beginning of the code.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In the first turn of the loop when you recalculate y you are using k1 .. k4 which have not yet assigned a value.
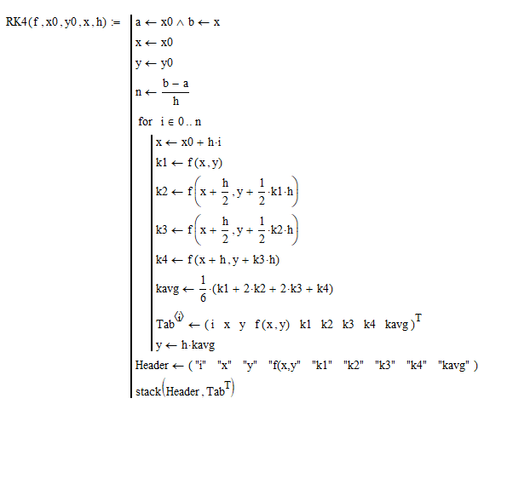
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks a lot. That was the way that the Results display to not interfere with the rows of mathematical part, such that to be only at the end rows. kavg is calculated only demonstratively to find out the average slope, I kept the original formula.
y - > y + (...)
At the first cycle, y will take always the previous value y = y0 that was declared before the cycle of FOR, ignoring (...).
Strictly by logical point of view is still correct, but indeed the programmers have their own patterns, procedures of building algorithms.