Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Goodness of fit (evaluate the significance of the models with correlation coefficients)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Goodness of fit (evaluate the significance of the models with correlation coefficients)
Hello,
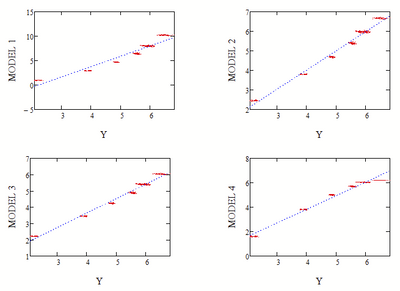
I have data X and Y. I have set up 4 different models for these data. I would like to evaluate the significance of the models. You can see in the graph that model 2 (green) is the best. I want to achieve this result not by looking, but by using a correlation coefficient.
My problem is that none of Mathcad's correlation coefficients give correct results. In Mathcad help, the Pearson correlation coefficient is often used for such purposes. From a workshop on Mathcad or from Wikipedia I know the general measure of determination. This provides plausible results. Only when the deviation is too large, as in model 1, does it deliver values greater than 1.
Does anyone have an idea why this is the case?
Thank you very much.
Best regards
Paul
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here are my 2 cents:
MeanSquaredError seems to give you a nice value to determine the best fit (lowest value).
Keep in mind that Pearson is a measure for linear correlation which might be the reason that model 2 has not the highest value. Its a measure for how good the data are near a straight line if you plot model... over Y (X is not used at all!). Given that, its looks by optical inspection that model 3 and model 2 have the best correlation in that respect:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here are my 2 cents:
MeanSquaredError seems to give you a nice value to determine the best fit (lowest value).
Keep in mind that Pearson is a measure for linear correlation which might be the reason that model 2 has not the highest value. Its a measure for how good the data are near a straight line if you plot model... over Y (X is not used at all!). Given that, its looks by optical inspection that model 3 and model 2 have the best correlation in that respect:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Werner,
Thank you very much for your help at this point. I will use the MSE. It is robust and simply defined.
Just because of my personal interest: I had also read it in several places that Pearson only works for linear equations. However, time and again I see Pearson being used for non-linear equations as well. For example, the QuickSheet in Mathcad 15 on logarithmic regression.
Then I had the following idea. You have linearised the models in your representation. I used this linearisation and inserted it into Pearson. Now it should be valid and deliver correct results. But the values increase to over 1. I can only explain this by the error that occurs when fitting the straight line.
Many thanks and best regards
Paul
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am not sure and out of my comfort zone here, but, as I understand it, Pearson is a measure for the linear correlation of two sets of (1-dimensional) data, in your case Y and modelx. What you have are two 2-dimensional point clouds Y over X and modelx over X. Not sure if Pearson as you had defined it could help here.