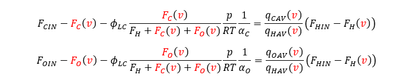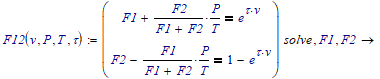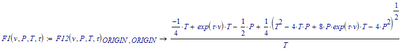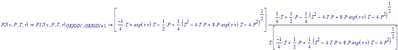Hi all,
I want to solve the following 2 equations for all v values:
Since there are 2 unkowns (Fo(v) and Fc(v)) and two equations, I want to obtain the Fo(v) and Fc(v) formulae since that should be possible.
I tried to find this formulae using the 'Find' function in mathcad prime:
However, that didn't work.
Attached you can find the worksheet.
Really appreciate your help in advance!
ACCEPTED SOLUTION
Accepted Solutions
@TW_9638511 wrote:
Since there are 2 unkowns (Fo(v) and Fc(v)) and two equations, I want to obtain the Fo(v) and Fc(v) formulae since that should be possible.
1) You have more than two unknowns because F.Cin, P and F.Oin had not been assigned any value
2) A solve block can only solve for variables, not for functions and you must solve for all unknowns, not just for the one of them which is of interest!
In the example below I assumed that you forgot to assign values for F.Cin, P and F.Oin and I assigned arbitrary values, exchanged the function you are looking for for simple variables (deleting the "(v)" after them), solved for both of them and then turned the solve block into a function depending on v. You can see how you can extract the single functions afterwards.
EDIT: Just noticed that Fred suggested a similar approach. had not seen his answer when I started my reply.
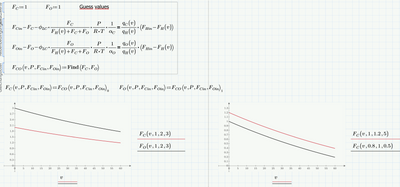
In case it was not a mistake that you did not assign values to F.Cin, P and F.Oin, you must make the function(s) dependent on those variables as well. The it looks more complicated and ugly but may have the advantage that you could compare the effect of changing those values - also in a single plot (like the one to the right).
Remark: Luc showed how to solve your system symbolically and he also showed that there is more than one solution. A numeric solve block as in my approach will only give you one solution and it depends on the guess values (I had chosen 1 for both variables) at which solution you will finally arrive at - so chose the guesses appropriately.
Worksheet in format Prime 6 attached
Prime cannot solve a solve block symbolically.
Enter your two equations in a vector and solve that symbolically. Here's an example:
Suppose you have
Then solve this
It results in a array function:
Note that (in this case) there are two possible solutions, the top row holds the first set of F1 and F2, which you can grab as follows:
The bottom row the other set.
It's up to you to select the proper set. In general, by inspection or by trial, you can rule out one solution set, because of inappropriate results (imaginary, negative, or the like).
Success!
Luc
You've got some unnecessary complications:
That won't stop the numeric solve block from solving. But you also have some undefined "constants"
that will stop a numeric evaluation cold. Need to fix those first.
Then to create numerically working functions, you turn the solve block into a function and write your function definitions below.
The red is because my Express can't run solve blocks, so it doesn't recognize things that full Prime would.
@TW_9638511 wrote:
Since there are 2 unkowns (Fo(v) and Fc(v)) and two equations, I want to obtain the Fo(v) and Fc(v) formulae since that should be possible.
1) You have more than two unknowns because F.Cin, P and F.Oin had not been assigned any value
2) A solve block can only solve for variables, not for functions and you must solve for all unknowns, not just for the one of them which is of interest!
In the example below I assumed that you forgot to assign values for F.Cin, P and F.Oin and I assigned arbitrary values, exchanged the function you are looking for for simple variables (deleting the "(v)" after them), solved for both of them and then turned the solve block into a function depending on v. You can see how you can extract the single functions afterwards.
EDIT: Just noticed that Fred suggested a similar approach. had not seen his answer when I started my reply.
In case it was not a mistake that you did not assign values to F.Cin, P and F.Oin, you must make the function(s) dependent on those variables as well. The it looks more complicated and ugly but may have the advantage that you could compare the effect of changing those values - also in a single plot (like the one to the right).
Remark: Luc showed how to solve your system symbolically and he also showed that there is more than one solution. A numeric solve block as in my approach will only give you one solution and it depends on the guess values (I had chosen 1 for both variables) at which solution you will finally arrive at - so chose the guesses appropriately.
Worksheet in format Prime 6 attached
