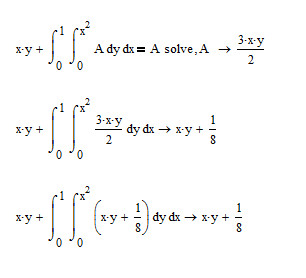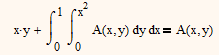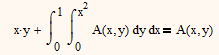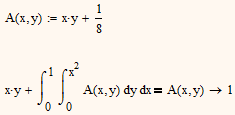Community Tip - Learn all about PTC Community Badges. Engage with PTC and see how many you can earn! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to explain this integral equation?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to explain this integral equation?
Just like the pic below:
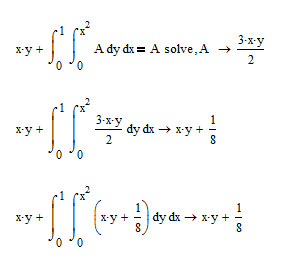
When I substitute the answer into the function, it give a different result but likely the true answer.
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad is right in its answer and then its not. The correct result of your first eval should be "no solution found".
The reason is, that your problem is an integral equation with A as a function in x and y (not A but A(x,y)) but the way you wrote is denotes that A would be a constant and so Mathcad treats it as such. The solution 3xy/2, which is obviously not a constant, means that there is no solution to the problem (no constant A).
Mathcad is not capable of solving differential equations symbolically nor will it solve integral equations at all.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
You should do one of the following, depending on your intent with regard to x:
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
But I think that zhu laojianke is trying to solve this equation:
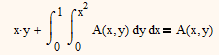
and he gives the solution himself with
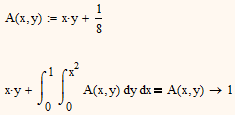
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
But I think that zhu laojianke is trying to solve this equation:
and he gives the solution himself with
Yes, Mathcad needs a little help with this. One needs to recognise that the integral term must evaluate to a constant, so one can assume A is of the form x.y+k (where k is a constant). Using this one can get Mathcad to solve for k (=1/8).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe the true result in the 3rd equation is a coincidence? Or, is there a way to solve differential equation by symbolic directly?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Or, is there a way to solve differential equation by symbolic directly?
As already written Mathcad offers no way to solve a DE symbolically but you may try Laplace transformation to get a symbolic result. It would require some manual substitution, though, unless you use Mathcad 11.
http://communities.ptc.com/docs/DOC-1394
http://www.ptc.com/appserver/wcms/resourcecenter/mathcad.jsp?im_dbkey=136068
http://ptc.hosted.jivesoftware.com/docs/DOC-3682
http://electronica.ugr.es/~amroldan/modulos/docencia/pfc/Mathcad/Laplace.pdf
Maybe the true result in the 3rd equation is a coincidence?
No, the "method" of first solving for a constant A and then feeding the (non-constant) result in the equation works for other functions and integral limits as well, as long as the double integral yields a constant, as is the case in your setup. I must confess that I am yet not quite sure why it works 😉 So I would prefer the method Alan had sketched.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If this is a bug on mathcad, I think this is a really useful bug!
It's easy than Laplace process even I don't know what the mathematical meaning of the tmp(x,y) and can not explain it.
Hehe, I'll test it and use it as a trick on solve a DE. ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What I had in mind is more along the lines of:
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
AlanStevens wrote:
What I had in mind is more along the lines of:
Yes, I know. I did it for demonstration in the last line of the screenshot for the second example as its the recommended way to do it.
Nevertheless I am unsure why zhu's three step procedure works - but then, I haven't thought about it much since my last post 😉
@Zhu: I turned your three steps into functions just for convenience so I would not be forced to change the function and integral limits three time when I was playing around. Tmp() is simply the result of your first line which is then fed into the equation. Again, I won't trust a method which is not standard math repertoire and which I don't understand, I dont't know why it works and especially I don't know when it works and when not.
Which DE are you trying to solve?
BTW, I don't understand what you think that a MC bug could be.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner:
I have tested this bug on several other pattern of integral equation and differential equation, and I have not found another example that it works, usually it can not find the answer. So fool am I...![]() This "bug" is only worked on this pattern of multiple definite integral function.
This "bug" is only worked on this pattern of multiple definite integral function.
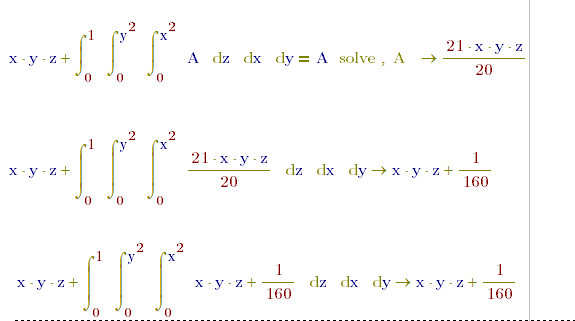
Different integrands get the same definite integral result, seems that there are multiple solutions with one definite integral function, or the answer of a integral definite equation is not unique, or different functions have same definite integral value. Just like the simple example below pic:
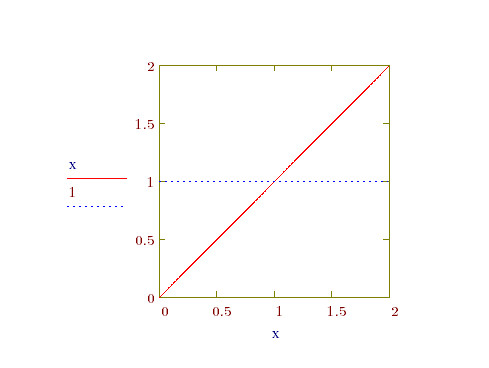
So the "3*x*y/2" is really the right answer of the equation. It seems not a bug, and the "A" is everything in symbolic solution not only constant in MathCAD.
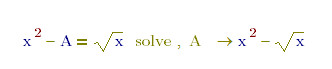
And since the answer of a definite function is not unique, I think to solve the integral function without constraint maybe meaningless for practical application.
Your and Alan's solutions are easy to understand. ![]()
zhulaojianke
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Sorry, my poor english, "the "A" is everything in symbolic solution not only constant in MathCAD", means:
The "A" is not only constant but everything in symbolic solution in Mathcad.