Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to iterate a cycle to converge
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to iterate a cycle to converge
Hello everyone,
I'm trying to create a way to iterate several equations of a dual cycle, in which I mainly guess for to variables. At the end I recalculate the variable I guess for and substitute the new value for the guess values until I get and error of 0.001. Yet, I can really find a way to make it simple and professional. Can anyone help me out or suggest a way or share an example? I would really appreciated.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Christian Eduardo Magno Marin wrote:
Hello everyone,
I'm trying to create a way to iterate several equations of a dual cycle, in which I mainly guess for to variables. At the end I recalculate the variable I guess for and substitute the new value for the guess values until I get and error of 0.001. Yet, I can really find a way to make it simple and professional. Can anyone help me out or suggest a way or share an example? I would really appreciated.
Do you need to iterate? I would probably look at a Mathcad Solve Block for this kind of problem - look "solve block" up in help.
If you do need to iterate, then it would be helpful if you could post your worksheet, as that means the Community could offer more specific and tailored advice.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's an example of Newton's iteration method to find a square root.
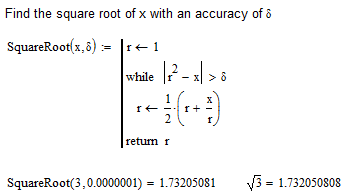
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Certainly, will be useful the following two examples. In the first, a transcendental equation is solved with the iterative algorithm of Newton. In the second one it solves a system of equations with the same iterative method but in several variables.
Greetings
F.M.

- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks StuartBruff, @LucMeekesand F.M. for the suggestions. I’m gona try them right now.
Okay StuartBruff, this is what I have at hand. I’m presented with a problem where I have a 6 cylinder CI engine and I’m given some data and a graph. The first part of the problem which I’m stuck on, is that I got to analyze the cycle of the engine, dual cycle. To initiate the cycle, I need to guess the value of xr and T1 and calculate every state. At the end, I use the data from the exhaust state and I calculate xr and T1. With the new xr, I calculate the error and it must be at least an error of 0.001%, if not I need to replace the calculated values with the guess and start again. Attach is the worksheet. With another program I got that the converging values would be T1=311.8 K and xr=0.01594, but I would like to develop the calculations in Mathcad that is why I’m trying to work it out. And again I appreciate any suggestions colleagues.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
See the attached worksheet. The solve block at the end does your iteration for you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks @Richard Jackson, it is very helpful.
But can you be kind to explain how does it work? Well how does it take the first calculated xr and T1 and recalculates? I mean, the whole time that I tried, I thought that I needed to put in the solve block all the equations that depended on the two variables. But I see that you only had to specified the variables that depended on xr and T1 and just on the solve block it was only needed to put the equations that calculate xr and T1. Also if I want the answer of a 5% error how would I specify that? Would I only have to change the default TOL? Also is there a way to see how many times does it iterate and the values of those iterations? Thanks in advance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For each expression that depends on the variable(s) of interest I made them functions of those variables. That way, they don't need any predefined values for those variables. You provide values when the functions are called. So there's a series of dependent functions down to your final expressions. In the final expressions you calculate new values of xr and T1 using the current values, and wished to do that until convergence. That is to say, until the LHS and the RHS are equal. Mathcad has numerical solvers that will do that for you. So I just turned your expressions into equalities (the bold equals), dropped them into a solve block, and told the solve block to find the values of xr and T1 that satisfy the equalities. Two equations, two unknowns.





