How to plot a triangle of XY-plane in 3-D for SURFACE PLOT (TO FILL COLOR) ?

[lvl107]

  Hello Everyone.
How to plot a triangle of XY-plane in 3-D FOR SURFACE PLOT IN ORDER TO "FILL (COLOR) SURFACE" TO THAT TRIANGLE ?
Thanks in advance for your time and help.
  Best Regards.

[Werner_E]

basically you have the choice between creating a polygon (a couple of point which may be connected by lines) or a surface patch.

MC15 sheet attached

EDIT: You added the need for a surface plot just after I replied. But you now have that solution, too.
BTW - no need to cry (capital letters)

[lvl107 · Accepted solution]

  I highly apprreciate your time and help, Werner. 😀😀😀. The method 2 that all I wish it.

     Many thanks, again.

          Best Regards.

               Loi.

[Werner_E]

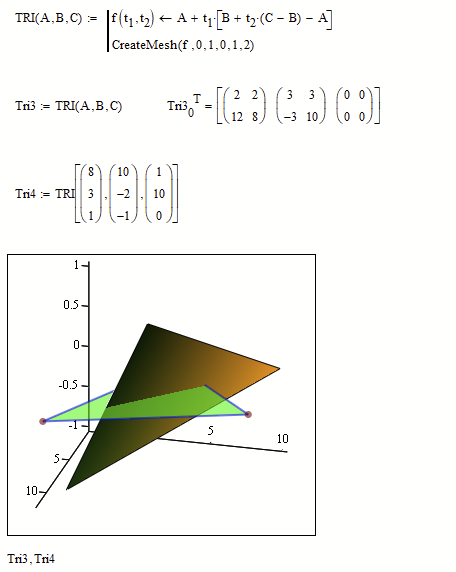
You may also use a functional approach and use CreateMesh()

[lvl107]

Thanks again, Werner. I guess this approach is better than the prior approach.(avoid hitting the wrong key-stroke)

    Regards.

[ValeryOchkov]

When I was a student, I solved such a problem in the discipline Descriptive Geometry (Engineering Graphics). Without a computer!
The coordinates of the vertices of three triangles are given. You need to draw them in three projections and find the coordinates of the common point, the intersection point of the triangles.

[Werner_E]

---

@ValeryOchkov wrote:

When I was a student, I solved such a problem in the discipline Descriptive Geometry (Engineering Graphics). Without a computer!
The coordinates of the vertices of three triangles are given. You need to draw them in three projections and find the coordinates of the common point, the intersection point of the triangles.

---

Ah yes, it was a long time ago, but I still remember it very well. And it was exactly those tasks I had in mind when I created that picture (where the penetration points are NOT constructed. The drawing relies on the correct visibility algorithm.).

The usual procedure was the "Deckgeradenprinzip" (I don't know how whats it called in English).
The procedure is explained step by step in this Powerpoint presentation: http://members.geometry.at/3d-geometry/Dokumente/deutsch/05_gak/05_08_06_te_a_schnitt_2dreiecke.ppsx

I loved Descriptive Geometry constructions, but a lot of what I learned got obsolete when computer geometry took over. Nevertheless, I believe that we were able to develop a better understanding through the tedious and time consuming constructions.

[ttokoro]