Community Tip - If community subscription notifications are filling up your inbox you can set up a daily digest and get all your notifications in a single email. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to plot the two equations
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to plot the two equations
Hi,
I want to plot the 2 equations in mathcad,
The two equations are,
2x^2+3y^2=59 (circle)
4y=x+8 (straight line)
these examples are used in Find command in mathcad.
I attached my code below.
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I want to plot the 2 equations in mathcad,
The problem is that Mathcad unfortunately is not able to plot implicit function. So you have to provide explicit functions or turn the equation into a parametric representation.
2x^2+3y^2=59 (circle)
Thats definitely not a circle but an ellipse!
these examples are used in Find command in mathcad.
Find uses an numeric algorithm an will only give you just one solution (depending on the guess values). Sometimes you have luck and the symbolic solve command will give you all solutions.
Here is a variation using just the symbolics (be aware that Mathcad's symbolic abilities are rather limited).

As you can see the ellipse is drawn as two plots (upper and lower half) and I have used a rather dense range variable x_ for plotting to avoid bigger gaps at the joints.
For plotting ellipses its much better to use a parametric representation which I guess cannot be found automatically but of course is well known for an ellipse.
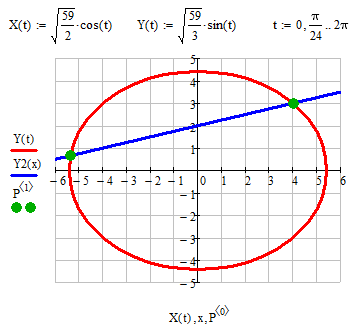
Regards, Werner
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I want to plot the 2 equations in mathcad,
The problem is that Mathcad unfortunately is not able to plot implicit function. So you have to provide explicit functions or turn the equation into a parametric representation.
2x^2+3y^2=59 (circle)
Thats definitely not a circle but an ellipse!
these examples are used in Find command in mathcad.
Find uses an numeric algorithm an will only give you just one solution (depending on the guess values). Sometimes you have luck and the symbolic solve command will give you all solutions.
Here is a variation using just the symbolics (be aware that Mathcad's symbolic abilities are rather limited).

As you can see the ellipse is drawn as two plots (upper and lower half) and I have used a rather dense range variable x_ for plotting to avoid bigger gaps at the joints.
For plotting ellipses its much better to use a parametric representation which I guess cannot be found automatically but of course is well known for an ellipse.

Regards, Werner





