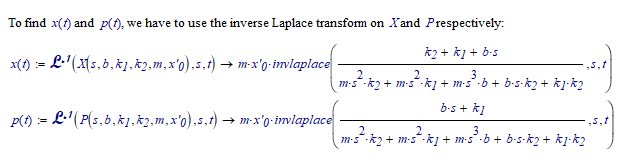Community Tip - Stay updated on what is happening on the PTC Community by subscribing to PTC Community Announcements. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
How to solve symbolic ODE system
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
How to solve symbolic ODE system
Hi everyone,
I'm trying to solve this EDO system, finding the solution for x(t) and p(t) with {k1,k2,b} symbolic variables and m=535:
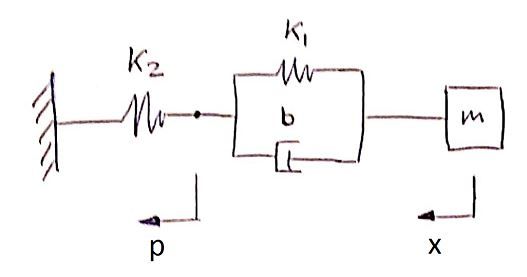
m*x''(t)=-k1*(x(t)-p(t))-b*(x'(t)-p'(t))
k2*p(t)=k1*(x(t)-p(t))+b*(x'(t)-p'(t))
Initial Conditions would be:
x(0)=0
p(0)=0
x'(0)=6.3
Already tried with Wolfram Alpha and Matlab, both giving solutions with terms "Root[#1^3+ (k1 m + k2 m) #1^2 + b^2 k2 m #1 + b^2 k1 k2 m^2&, 1]" in which I don't understand what is represented. Examples attached in following pictures:
Matlab:
- Labels:
-
Calculus_Derivatives
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad can solve ODEs only numerically, not symbolically.
The "Root" you see in the symbolic solutions of Matlab and Wolfram possibly is the solution of a cubic equation which cannot be given in a closed form as its form depends on the values of the various constants.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Seems like Maple will give an explicit solution without any Root's
Here's the commands
The full result in in the attached PDF
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's how you could (try to) solve it:
So now we have X and P...
And that's where it becomes a little problematic. You have to take the inverse Laplace transform of a ratio of polynomes where the order of the denomonator polynome is 3. This is not easy, but apparently modern Maple can do it, as Mvenich shows. I've entered one of the two expressions in WolframAlpha, to find a similar expression involving the root() function:
Conclusion: there's no simple closed form.
However...
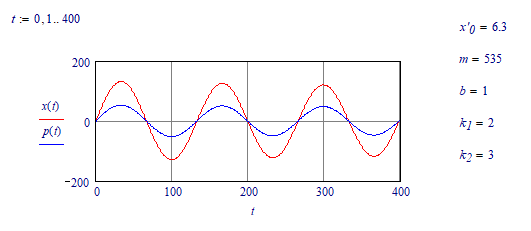
Success!
Luc
P.S. I suppose this timeline is more interesting: