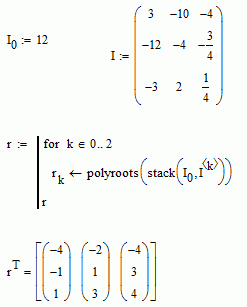Community Tip - Learn all about the Community Ranking System, a fun gamification element of the PTC Community. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
I am writing a program to calculate principal stresses from stress tensors. The principal stresses are defined by a cubic equation. The invariants (coefficients) of the cubic equation are calculated from stress tensors. The stress tensors are first rea
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I am writing a program to calculate principal stresses from stress tensors. The principal stresses are defined by a cubic equation. The invariants (coefficients) of the cubic equation are calculated from stress tensors. The stress tensors are first rea
I am writing a program to calculate principal stresses from stress tensors. The principal stresses are defined by a cubic equation. The invariants (coefficients) of the cubic equation are calculated from stress tensors. The stress tensors are first read into Mathcad from a multi-row file of stress tensors. Each row represents a state of stress at a node in a finite element model. There are six stress tensors for each row in the file. I am able to read the file row by row and assign the stress tensors to a matrix. From the stress tensor matrix I am able to calculate the invariants (there are three invariants , I1, I2 and I3, plus a constant term, I0, for each row of tensors) and assign each invariant to a separate vector having as many rows as nodes of interest.
What I have not yet been able to do is calculate the three roots of the cubic equation that define the principal stresses and output a matrix populated with the results by looping through each row of data. The attached program graphic attempts to do this, but does not work. First, I define a cubic polynomial for each node using the calculated invariants. Then I extract the coefficients from the cubic polynomial and assign them to a vector v. I then use the polyroots function to solve for the roots of the cubic equation and assign the solution (roots) to the vector r. The vector r contains the principal stresses I desire. The last three lines of code rearrange the order of principal stress solution in vector r and populate the matrix prinstress. The end goal is to have the matrix prinstress available for inspection and further processing in Mathcad. What change is required to the program below to generate the result I desire?
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Bradley.
That's? If it is, use column extractor for matrices (M^<> in the toolbar).
Best regards.
Alvaro.