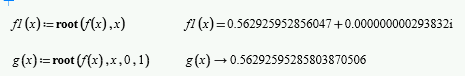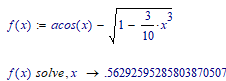Community Tip - Your Friends List is a way to easily have access to the community members that you interact with the most! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
I use different method to get same answers but one of the method did not working.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I use different method to get same answers but one of the method did not working.
Hello PTC fam,
I'm quite in a bind here where as my result in pic 1 doesn't give the same answer like pic 2 and pic 3. Here I attached my pictures in program. I don't know where I did wrong since it suddenly have the "i" thing there. Thanks in advance.
Regards,
Adlil
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Adlil wrote:
Hello PTC fam,
I'm quite in a bind here where as my result in pic 1 doesn't give the same answer like pic 2 and pic 3. Here I attached my pictures in program. I don't know where I did wrong since it suddenly have the "i" thing there. Thanks in advance.
Regards,
Adlil
I'm not sure that you did anything wrong. I haven't got Mathcad 15, but converting it to Mathcad Prime 8 shows the same result for all 3 versions.
The "i" is simply the imaginary number, indicating that method 1 (pic 1) is returning a complex number. I suspect that this is due to the way that Mathcad 15 calculates root. Given that it's a numerical method, there is probably some round-off error that makes root think there is a very small imaginary component - in the order of 10^-13 or so. Change the number of decimal places that you're showing and see if that shows some trailing digits (other than zero!).
Another thing to try is using the symbolic processor (you'll need to add a pair of limit values, say 0 and 1, to root).
Here's what Mathcad Prime 8 shows for 15-digits (the imaginary element doesn't show for 4 or 5 digits in Prime😞
Stuart
(PS - please use the "Insert Photos" button to add pictures to a message. This will (should) automatically display the images in the text, thus making it easier for the reader to see them)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Adlil wrote:
Hello PTC fam,
I'm quite in a bind here where as my result in pic 1 doesn't give the same answer like pic 2 and pic 3. Here I attached my pictures in program. I don't know where I did wrong since it suddenly have the "i" thing there. Thanks in advance.
Regards,
Adlil
I'm not sure that you did anything wrong. I haven't got Mathcad 15, but converting it to Mathcad Prime 8 shows the same result for all 3 versions.
The "i" is simply the imaginary number, indicating that method 1 (pic 1) is returning a complex number. I suspect that this is due to the way that Mathcad 15 calculates root. Given that it's a numerical method, there is probably some round-off error that makes root think there is a very small imaginary component - in the order of 10^-13 or so. Change the number of decimal places that you're showing and see if that shows some trailing digits (other than zero!).
Another thing to try is using the symbolic processor (you'll need to add a pair of limit values, say 0 and 1, to root).
Here's what Mathcad Prime 8 shows for 15-digits (the imaginary element doesn't show for 4 or 5 digits in Prime😞
Stuart
(PS - please use the "Insert Photos" button to add pictures to a message. This will (should) automatically display the images in the text, thus making it easier for the reader to see them)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Omg, thank you so much. I just did like you suggest and get the answer exactly like the other method. It seems I just need to add limit values. I think it happens with imaginary number because it got no limit and calculate for all possibilities (not sure if my understanding is correct or not). Thanks a bunch. Appreciate it.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Adlil wrote:
Omg, thank you so much. I just did like you suggest and get the answer exactly like the other method. It seems I just need to add limit values. I think it happens with imaginary number because it got no limit and calculate for all possibilities (not sure if my understanding is correct or not). Thanks a bunch. Appreciate it.
No worries. Yes, root will likely examine a larger solution space and end up with a "good enough" solution when approaching the "correct" answer from somewhere in the complex plane (off the real axis). As you say, adding the limits constrains the solution space.
Stuart
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The symbolic processor should be able to find the root without a pair of limits. Just:
Success!
Luc