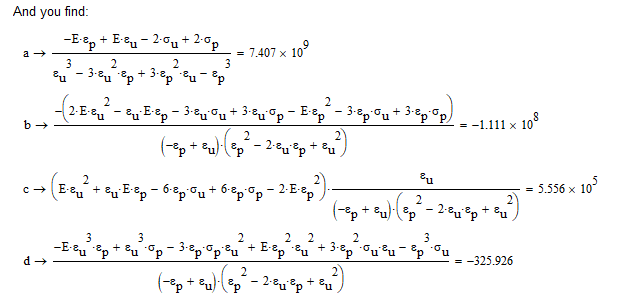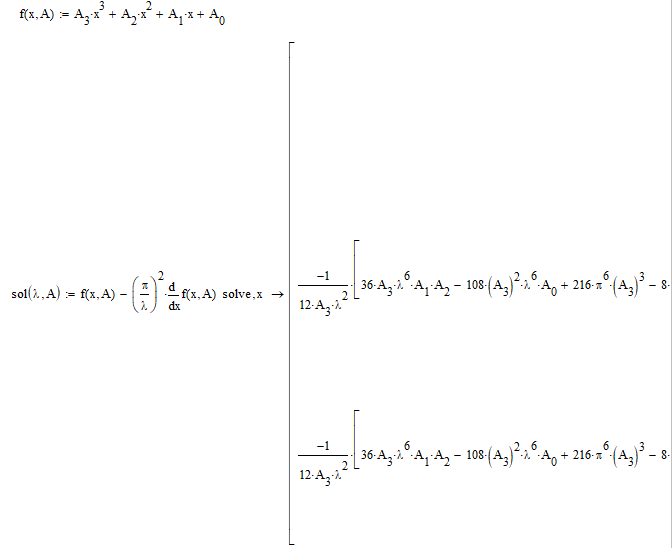Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
I want to solve for X a cubic equation that contains a vector as an input
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I want to solve for X a cubic equation that contains a vector as an input
I am trying to solve a cubic equation for the unknown X, but one of the input parameters is a vector. I tried to solve symbolically and then substitute the vector but something doesn't seem right. Then i tried to program a function that solves it for every value of the vector input, but since the result contains 3 solutions, it doesn't work.
I hope you will be able to find a solution.
Thank you in advance.
P.S. The file is uploaded
Solved! Go to Solution.
- Labels:
-
Physics
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The attached sheet should help.
Personally I would prefer the "numerics only" solution at the end as I see no need for using the symbolics.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The attached sheet should help.
Personally I would prefer the "numerics only" solution at the end as I see no need for using the symbolics.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Perfect solutions. I couldn't find even one.
Thank you very much to you and all others who helped.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is this what you are after?
(The symbolic result stretches out further to the right)
I prefer a symbolic solution in general, because it can provide more insight...
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc!
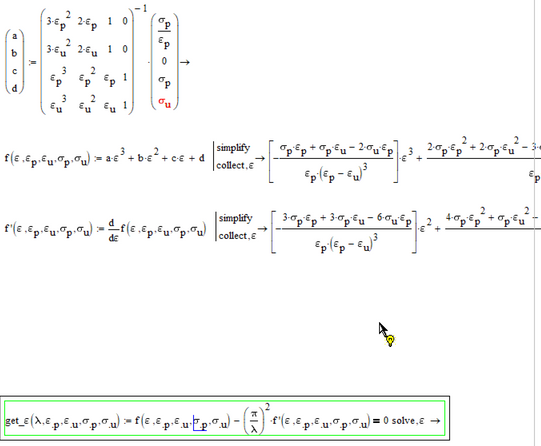
Guess you misunderstood the question. The calculation of a,b,c,d was done somewhat awkward in the OPs sheet, but the question was about the cubic equation which was based on the calculated values of a,b,c,d.
The one with f(eps) and its derivative and with the parameter lambda.
Guess the throughout symbolic solution for this equation will look quite ... interesting 😉
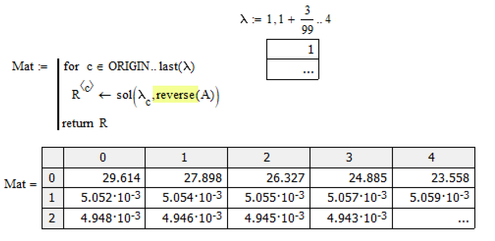
Main question as I understood was how to solve this cubic for a 100 element vector of lambda-values and how to arrange the result in a 3 x 100 matrix.
EDIT
A true symbolic solution could be something shown in the following screenshot. I didn't wait for the calculation to finish and i doubt that the solution (should calculation ever should finish without crashing the program or throwing an error) would provide more insight 😉
EDIT2:
I had Mathcad running while typing this and after sending the post I was confronted with an "out of memory" error. I won't try it in Prime as I think that even though Prime could benefit from the full memory in my machine, and even if Prime could finish this calculation, the result expressions would not be of much help.
Maybe Maple in MC11 has more success, maybe some assumptions like ALL=real or ALL>0 can help.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, it couldn't have been as simple as that.
I've looked a little further and came to this (continuing from the previous):
Again, this solution runs far into the right. It's the general solution for a third-order polynome.It gives 3 values for each lambda..
With the result I can continue:
This solution (e.g. for lambda=1) is different from what you find. Where do I go wrong?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This solution (e.g. for lambda=1) is different from what you find. Where do I go wrong?
You reversed the order of the coefficients. In the setup of the OP a should denote the coefficient of x^3, in yours its the coeff of x^0. Doing the reverse (better define A differently) and providing the same vector for lambda the results match.
Nevertheless I'd still vote for a pure numeric solution via "polyroots". I have streamlined mine a little bit - no need for that auxiliary function.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, So I only need to correct the last part:
And yes, the full symbolic solution of sol(lambda,A) can be obtained, but is uncomfortably large.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And yes, the full symbolic solution of sol(lambda,A) can be obtained, but is uncomfortably large.
Aha, so once again Maple in MC11 rules.
Here is one of the most compact and fully complete ways to get the desired table (using numerics only):