Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Imaginary Exponent : (x^1i)^1i
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Imaginary Exponent : (x^1i)^1i
Hello, Everyone.
Thanks in advance for your time and help.
Best Regards.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is this any help?
What motivates these questions of yours?
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmmm, this not only assumes that x is real but its also only one out of an infinite number of "solutions" for (x^i)^i.
In the complex domain we run into ambiguities quite often and easy and rules for calculating with powers etc. not always apply the same way as in domain real. That was the fine thing with MC11 and Maple - it defaults to domain real and most of the time simplified expressions the same way we would do (using some implicit assumptions).
The current Mathcad's muPad can't even simplify (2^i)^i to 1/2 wheras the numerics has no problem
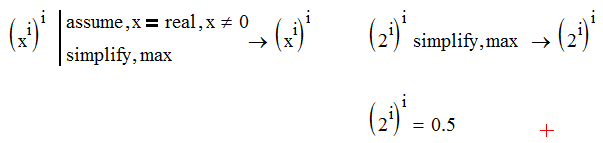
muPad obviously thinks more complex (pun intended):

and so we have multiple ways to express (x^i)^i and Mathcad can't simplify to the one with k=0. I'd wish that MC would at least give the simplification similar to my expression. Mathcad will usually do so with "solve,fully" but in this case with no success
![]()
We can "verify" the multiple "solutions" with the numerics (the symbolics again is of no help, possibly again as of other ambiguities)

Just noticed that also Mathcads numerics does NOT simplify that expression to 1/x. Thats the reason for the strange lookin plots with all its jumps

What motivates these questions of yours?
Yes, this would also be of interest to me. Loi Le is around here for some years with his special questions and I also asked few times about the reason or the source of his various problems but unfortunately never got an answer.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Werner Exinger wrote:
Hmmm, this not only assumes that x is real but its also only one out of an infinite number of "solutions" for (x^i)^i.
Quite right. But, at best, Mathcad is never going to give more than the simplest solution to these sort of questions (any more than it gives an infinite number of solutions to arcsine(theta), say), so I stuck to the simplest!
That said, your reply is likely to be more useful than mine to Loi Le if he's just trying to educate himself about these relationships - where just relying on software could be misleading.
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I guess Loi Le already thought that his expression could be simplified to 1/x (using the rules for real variables) and was confused as of the graph mathcad was delivering. Took me a while, too realize whats going on. The graph with logarithm scale should clarify things, I hope.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And a related question :
Thanks in advance for your time and help.
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Which (x^i)^i are you asking for - we have an infinite number of them - see my other post.
But for every of those hyperbolas is the answer the same - obviously Min and Max are +/- infinity
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for your time and help, Alan and Werner. ![]()
With the Graph, above, I guess :
since :
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I think you dont understand what I meant with ambiguity.
(x^i)^i is not 1 curve but this expression represents an infinite number of curves. The numeric choses one of them depending on th x-value. You have a jump from (1/x)*exp((k-1)*2*pi) to (1/x)*exp((k)*2*pi) at x=exp(2*k-1) for every integer k. So the highest value which Mathcad would yield is exp(pi)=23.141, but thats insignificant. If x approaches zero the "jump points" accumulate.
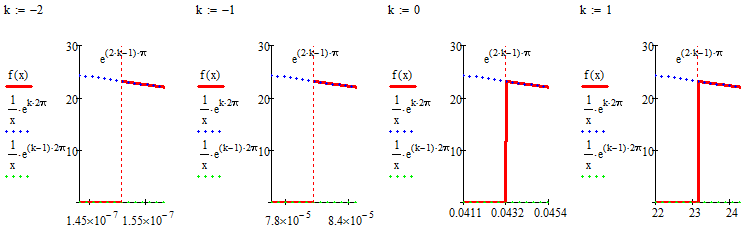
Don't you think it would be time to tell us where your problems stem from and what you are trying to do?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
All are just my intuition ( and hobby for recreation for spare time ).
Best Regards.
Loi Le.
Werner Exinger wrote:
Don't you think it would be time to tell us where your problems stem from and what you are trying to do?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I see, but isn't there anything you want to achieve? Or is it simply to explore Mathcad and show its sometimes weak symbolics? I guess you knew, or better you thought to known, that (x^1i)^1i ressembles 1/x. As I have shown this isn't true because some calculation rules aren't valid in the domain complex.
Anyway, here is for your information a plot of "your" function (better: relation) with logarithmic scaled abscissa. You see the jumps evenly spread in constant relative distance (in my last post I was missing a pi when I gave the x-values for those jumps; see the file for the correct expression). The blue dotted lines are the various hyperbolas which are all the real graphs of your function. The red curve represents the values Mathcad decided to chose. The study of that curve doesn't make much sense in my opinion.
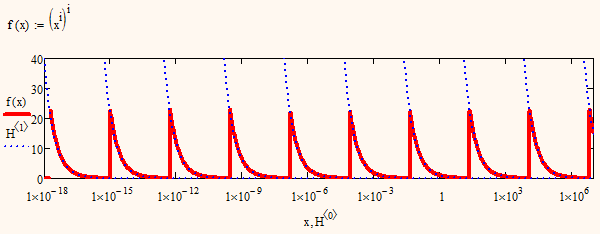
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And another relative question :
Thanks in advance for your time and help.
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems you didn't really understood my remarks about the mathematical ambiguity of the function in question and the way Mathcad deals with it and I honestly can't think of anything better to explain than the plot in my last post.
I already showed that from the mathematical point of view we have
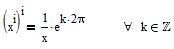
So your equation has an infinite number of solutions:
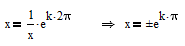
Mathcad (practical math??) will give you just the two solutions +1 and -1, depending on the guess value you provide. For some guesses you may even get 23.141 (=exp(1*pi)) because Mathcad ran into some kind of numerical inaccuracy.
I guess that this will be my last reply to this and "related" "problems".
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
And it seems that I am wrong with the following :
Best Regards.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator





