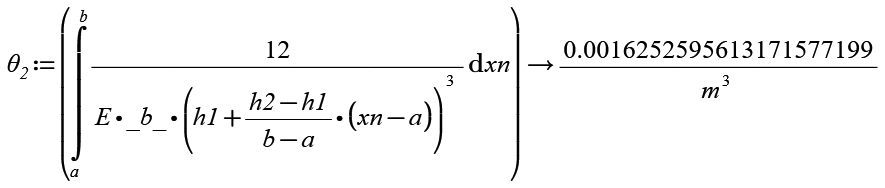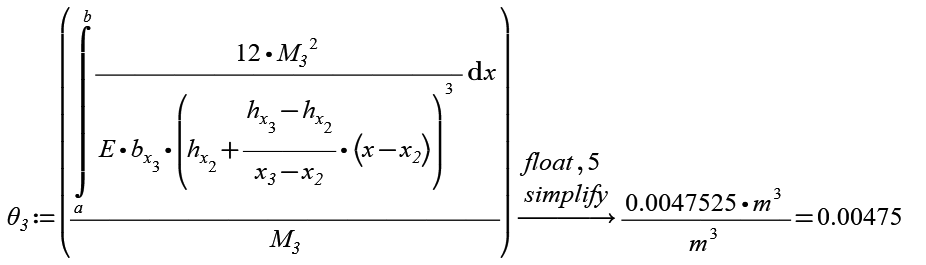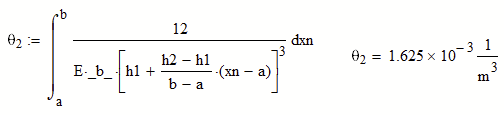Community Tip - Have a PTC product question you need answered fast? Chances are someone has asked it before. Learn about the community search. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Integral Function Fails to Solve
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Integral Function Fails to Solve
FOR A REASON OR ANOTHER THE SOLVER DOESN'T PERFORM THE INTEGRATION.
The program is typically solving for Int [a to b] (Ax+B)^(-3) dx.
--------However, I have several Matrices defined.-------
Initially the first matrix in the Integrand function resulted in errror : <Not a Singular Matrix.>
Thus recognizing the matrix as x, I redefined x as xn, and dxn. Please see Theta2 equation.
I know the solution, I wish for the program to simplify future problems.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Not sure if thats what you'd like to achieve, but why do you use symbolic evaluations? You quickly get the numeric result by using the normal numeric evaluation (=)
In case of theta1 you did not defined E and so you see E in the symbolic result. If this was a mistake, then define E and again use numeric eval. If it was no mistake you could make theta1 a function of E and (numerically) evaluate at various values for E if thats what you are after.
BTW, I guess the reason why the symbolics fails are the units of the integral limits. The symbolics doesn't know anything about units!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
No Sabía :: I didn't know
@Werner_E wrote:
Not sure if thats what you'd like to achieve, but why do you use symbolic evaluations? You quickly get the numeric result by using the normal numeric evaluation (=)
In case of theta1 you did not defined E and so you see E in the symbolic result. If this was a mistake, then define E and again use numeric eval. If it was no mistake you could make theta1 a function of E and (numerically) evaluate at various values for E if thats what you are after.
BTW, I guess the reason why the symbolics fails are the units of the integral limits. The symbolics doesn't know anything about units!
"The symbolics doesn't know anything about units!"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Prime7
Without units "m" and x2:=x[2 and x3:=x[3
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
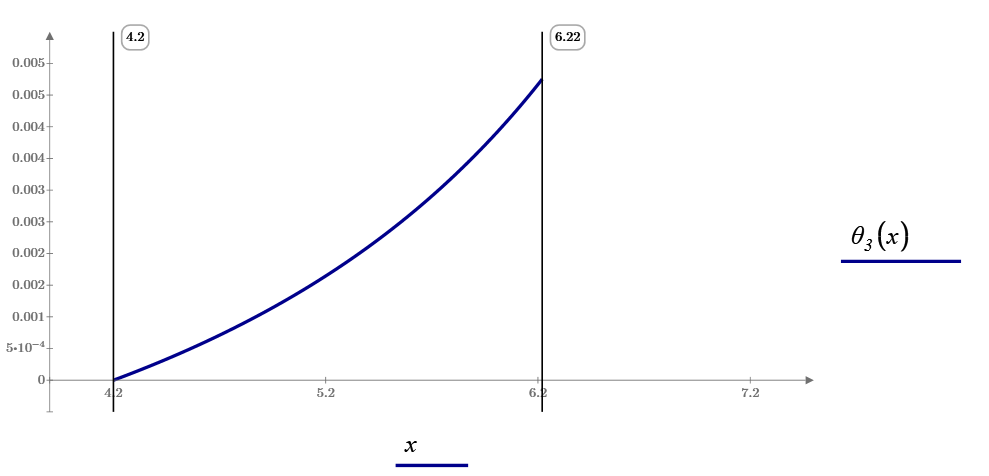
Plotting the result, check the equation what you want.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My two cents.
This will help if:
- you want to know how the result of this integral depends on the parameter values of the function, or
- you need the result of this integral for many sets of parameter values.
- you need the result of the integral to be maximally accurate (Note that numerical integration results in an approximation).
It will NOT help if the integral has no symbolic solution.
But if you are only interested in numerical result of a single evaluation, you may be better off not using symbolics.
Success!
Luc