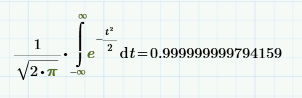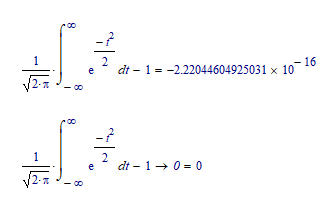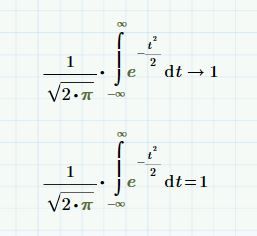Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Is the calculation accuracy low in MathCAD compared with Maple?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Is the calculation accuracy low in MathCAD compared with Maple?
I met some problems on calculation accuracy in MathCAD, I hope friends in this forum could help me.
I really appreciate your help.
Solved! Go to Solution.
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The differences you see are due to numerical approximations (when you use a numerical evaluation with '=').
If you let Mathcad solve your problems symbolically you get exact answers. In your examples with Maple, it determines the solutions symbolically, then (when needed) it converts the answers to numerical answers.
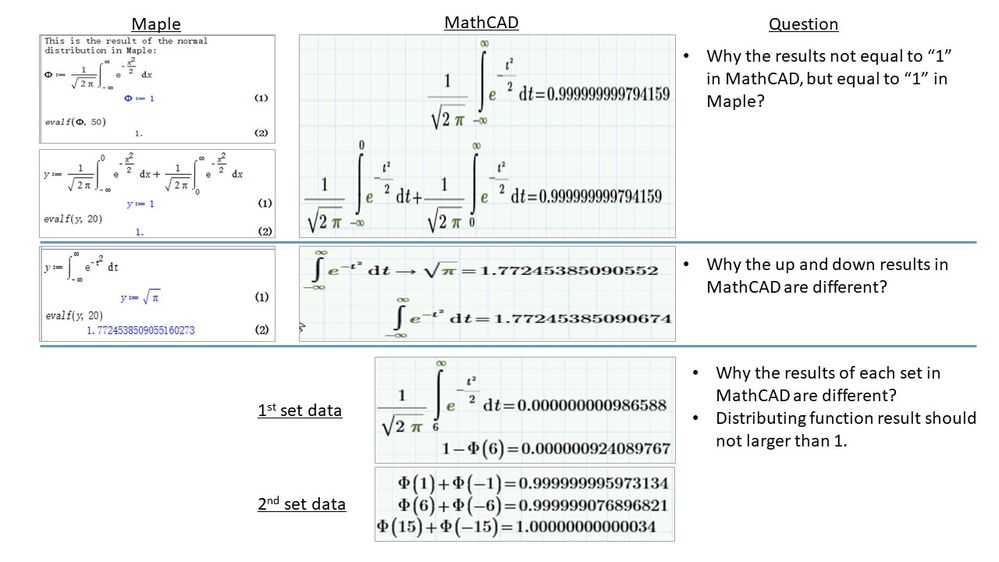
The example above from Fred appears to show an exact match between the numerical approximation and the symbolical solution of the integral over the normal distribution function. But when you tell Prime to show the result with sufficient decimals (15...) then you see the answer is not eactly 1:
(This was done with Prime 4.0 express, hence I cannot show the symbolic result.)
In Mathcad 11 (which uses Maple as its symbolic engine) you get:
(If I tell Mathcad 11 to show 15 decimals, it still shows 1 as a numerical result. To show the 'error' I had to subtract 1 from the integral).
Apparently the numerical approximation is done differently from Prime's algorithm, or the settings are different, resulting in a somewhat better approximation of 1 for the integral.
Note that the symbolic result is exact.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In Prime 3.0, (paid for) I get:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Fred,
Thank you for your help.
--
Jeff
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The differences you see are due to numerical approximations (when you use a numerical evaluation with '=').
If you let Mathcad solve your problems symbolically you get exact answers. In your examples with Maple, it determines the solutions symbolically, then (when needed) it converts the answers to numerical answers.
The example above from Fred appears to show an exact match between the numerical approximation and the symbolical solution of the integral over the normal distribution function. But when you tell Prime to show the result with sufficient decimals (15...) then you see the answer is not eactly 1:
(This was done with Prime 4.0 express, hence I cannot show the symbolic result.)
In Mathcad 11 (which uses Maple as its symbolic engine) you get:
(If I tell Mathcad 11 to show 15 decimals, it still shows 1 as a numerical result. To show the 'error' I had to subtract 1 from the integral).
Apparently the numerical approximation is done differently from Prime's algorithm, or the settings are different, resulting in a somewhat better approximation of 1 for the integral.
Note that the symbolic result is exact.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Luc,
Thank you for patient answer the question, solve the problems, i was deeply touched.
I think i will never eaisy suspect the calculation accuracy of CAS because of my poor knowledge foundation.
--
Jeff
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For exact results you should use symolic evaluations only:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi Werner,
Yes, i redefine the Φ(x) for normal distrubtion function. Really thank you for your guide.
--
Jeff