We are aware of an issue causing pages to load incorrectly for some users and expect a fix soon. Sorry for the inconvenience.
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Laplace Circuit Analysis "Replace complex values and NaNs by real numbers"
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Laplace Circuit Analysis "Replace complex values and NaNs by real numbers"
Hi,
I'm trying to make a template that can be used for circuit analysing using Laplace transform.
Here, we have a second order RC lowpass filter and I want to use an repetitive input signal.
In V2(s) equation, where we have the input voltage I would like to use the f(s) input function or even better g(s) repetitive input function.
In the file attached you can see that I have 3 plots: one with input voltage as a constant, where it works and the plot is ok, and another two using f(s) and g(s), where it returns this error "Replace complex values and NaNs by real numbers".
What can be improved in order to use the repetitive s domain function?
Mathcad using is Prime 4 and you cand find attached a .pdf too.
Thanks.
- Labels:
-
Electrical_Engineering
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Try to evaluate V.2_f for, lets say, t=10^-5, numerically!
You run into an overflow error - the calculation of a subexpression yields a result greater than the numerical limit of 10^307 and throws an error.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
Although realized with mathcad15, you can rewrite it in Prime. You should proceed in this way:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I enclose the Mathcad 15 worksheet related to your problem and which you can easily import into Prime. Learn the art and put it aside...
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi -MF-,
If i rewrite your input signal, when I try to plot returns the following error: "This value must be a real number"
LE: I solved this step, I will go on and return with news.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
It is not necessary to rewrite the whole worksheet. It is sufficient and very fast (a few seconds) to import the file into Prime. Then you have to do some adaptation.
If you've already done it, did you import the file in Prime correctly?
(Vsqw is dimensionless while V.sqw isn't.)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello again -MF-,
Sorry all for my slow reply.
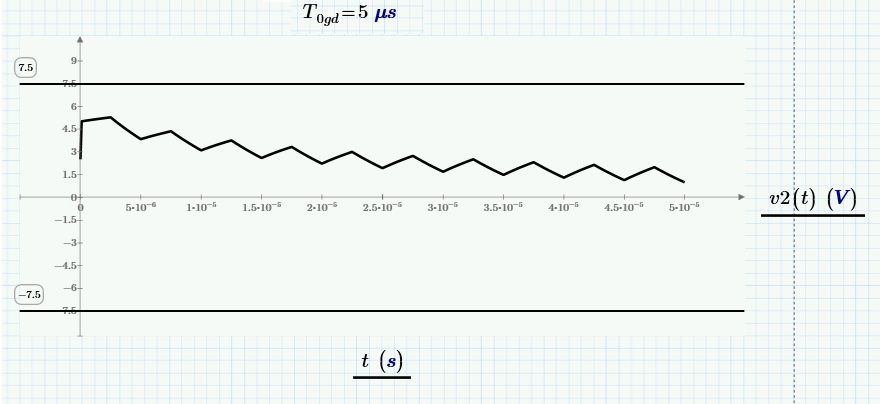
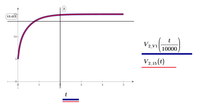
Yes I imported as you shown but it does't have the same result. See picture attached
Thank you.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
You have to check that the labels are the correct ones.
In any case, I attach the mcdx file.
In the graph there is a small anomaly (circled in red) to be corrected.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
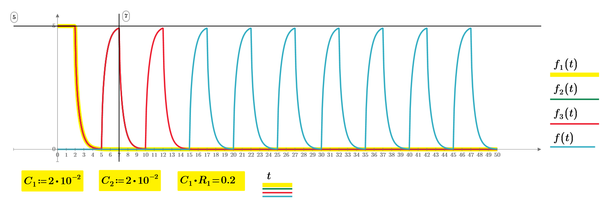
If C=2*10^-6 then tau is 10000 times faster than my result as already Werner_E wrote.
So the output signal shape is same to input waveform, 5(u(t)-u(t-2)).
My results change the C to 2*10^-2, therefore, transient change in output signal is visible. However, Prime 5 of my devise only solve one or two input series of inverse Laplace transformation. It can also solve numerically three input pulse series. Therefore, I made the 3rd response as a series of rest 7 pulse responses.
Because the 1st to 2nd responses after the 3rd response is too small to affect the results in my graph scales.