Community Tip - Did you get called away in the middle of writing a post? Don't worry you can find your unfinished post later in the Drafts section of your profile page. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Malfatti circles
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Malfatti circles
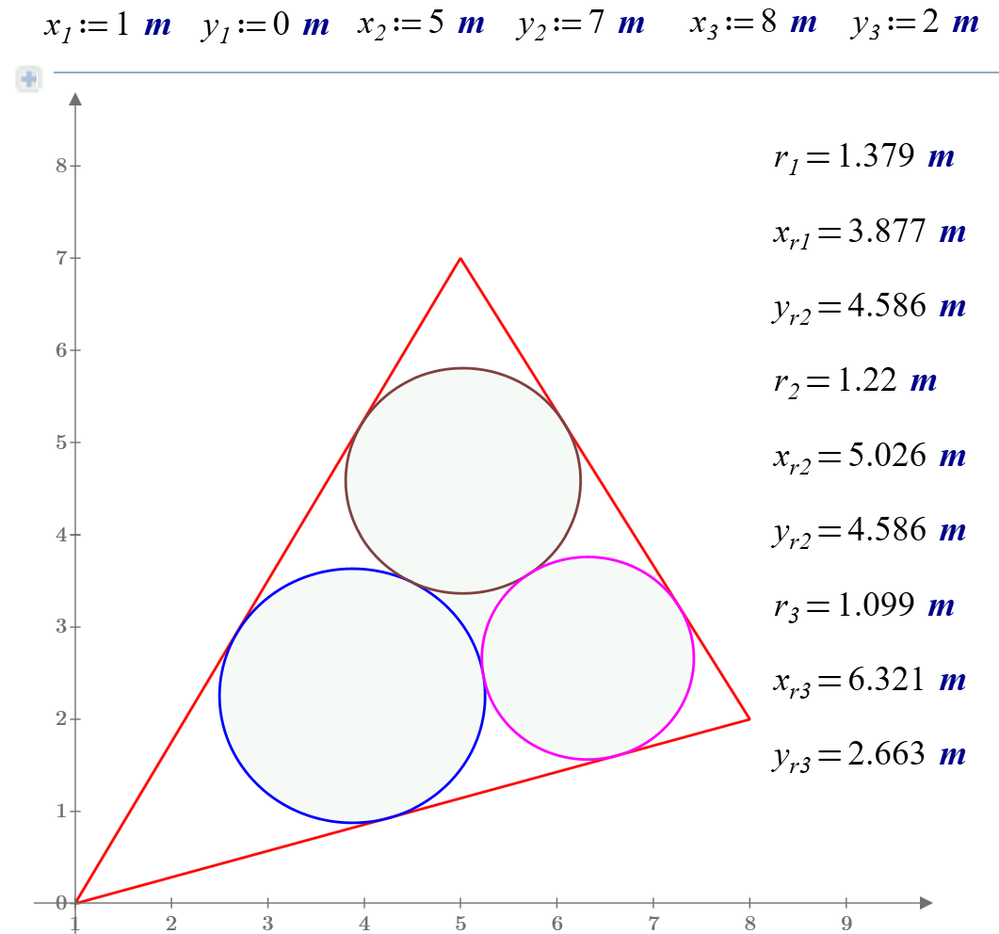
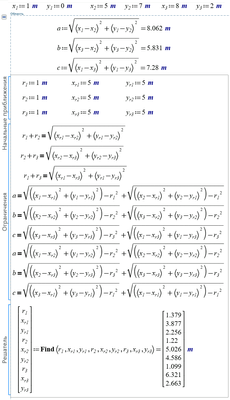
I have solved the
with Prime 6 or Mathcad 15 - see pls attach
Can you solve it more sort, more nice 😉
- Labels:
-
Algebra_Geometry
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
There is a long-serving regular contributor here in the forum who likes to comment on such occasions that a solution without animation would not be a solution.
You may have read it here once or twice (or was it 100 times?). 😈
I apologize as this is neither a particularly beautiful nor a particularly useful animation.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, not each animation is informative and useful.
I hope this is more interesting - an animation of the numeric solution
one connected problem.
Let's wait for other decisions, and then open our playing cards, sorry, our solutions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, we have already seen this animation in the past.
Thought that the Malfatti circles would be a nice task for some kind of genetic algorithm for you to implement.
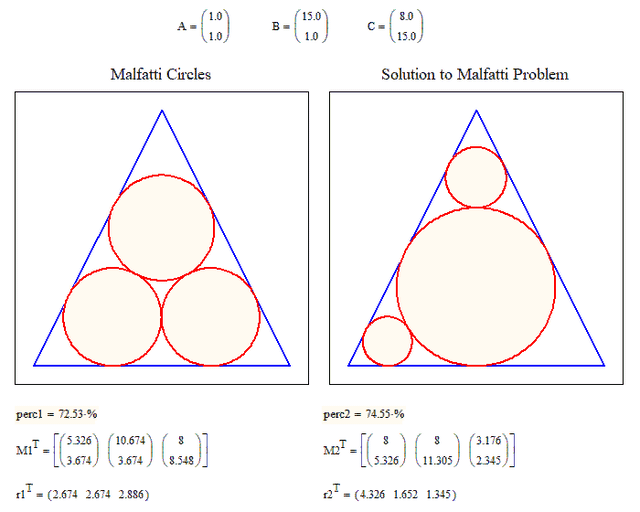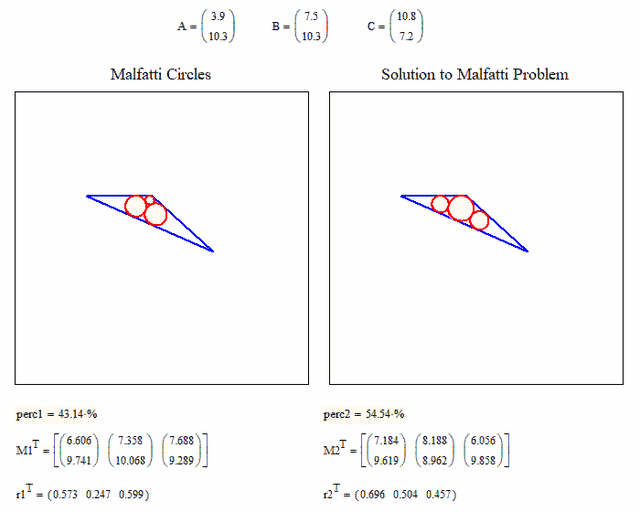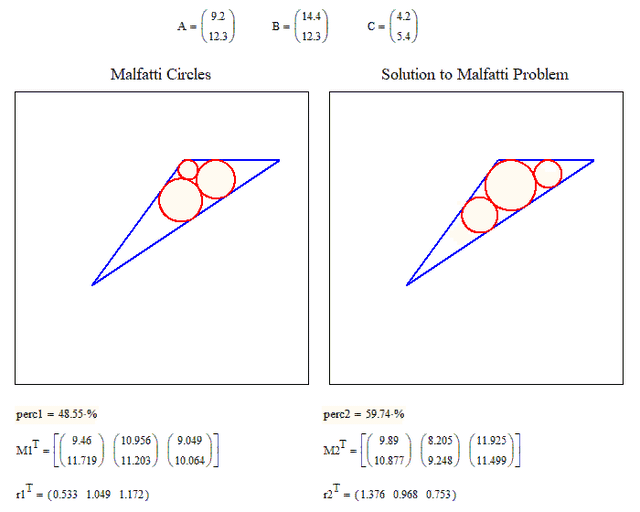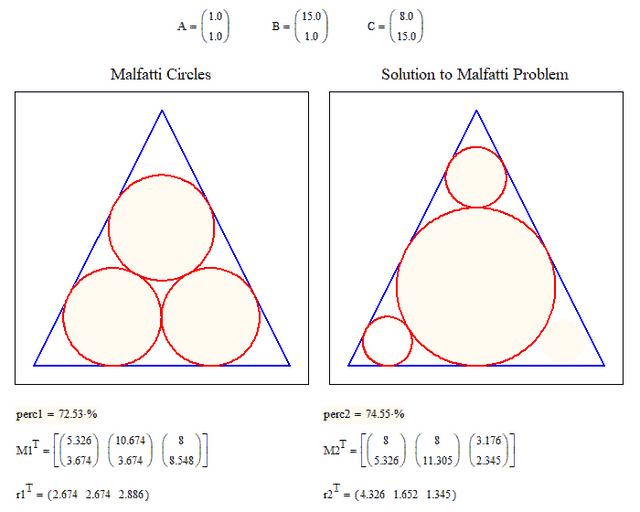
It also would be nice to compare the Malfatti circles to the solution of the Malfatti problem side by side. You probably know that it was proven that the Malfatti circles never are solutions for the Malfatti problem.
The Malfatti problem consists in finding the three inscribed and not overlapping circles with the largest area sum. It can be proven that a simple greedy algorithm does the job.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Now, if you can do that animation in Prime , , ,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Главный русский принцип:
Если нельзя, но очень хочется, то можно!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
...Express ! (?)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@Fred_Kohlhepp wrote:
Now, if you can do that animation in Prime , , ,
I see no reason for using Prime for anything as long as I have access to real Mathcad 😉
I remember that Valery once posted a simple animation done by manually put together a couple of screenshots.
I guess nice animations even with Prime could be done and and be automated to a large part by using a script language like AutoIt. It can take screenshots of areas you define, can operate Prime, change variables there, etc. But it sure would involve quite some work to make it run. But once you get the hang of it, this approach would open up a lot more possibilities than the simple MC15 animations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here you can compare the percentage of the triangle area covered by the Malfatti circles and the true solution of the Malfatti problem (maximum covered area by three circles). It demonstrates that the Malfatti circles never are solutions to the Malfatti problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Super! Can you show Mathcad-sheets? I will do it too.
And what about a tetrahedron and three spheres?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Super! Can you show Mathcad-sheets?
Sure, there is nothing confidential or secret in my sheet.
Here you are. The MC15 file is attached. Have fun!
And what about a tetrahedron and three spheres?
Why just three? Wouldn't four be more appropriate? Looking forward to see your solution 😉
I guess that the solution for this 3D Malfatti problem (maximize the volume of the spheres) would be easier to solve (greedy algorithm) than the 3D generalization of the Malfatti circles (the spheres all being tangent to each other and to the tetrahedron sides). Proving that a greedy algorithm gives the solution for the maximum volume would be another thing. The prove for the 2D problem is 25 pages and also involves computer calculations to deal with all relevant constellations.
In case you are really interested in a high dimensional generalization of Malfatti's problem, you may check this
https://www.aimsciences.org/article/exportPdf?id=c026650a-cc3b-4ec0-9a6a-d729ccf92bdc
or this
http://www.aimsciences.org/article/id/0953c355-7831-43ea-9412-0fdcb8f9b5a7
A classic generalization of the Malfatti circles is to change the straight triangle sides for circle arcs.
I now found an interesting paper where the Malfatti circles were generalized (still in 2D) in a new way. The task is to fit six circles into the triangle, tangent to each other and to the triangle sides. Of course "tangent to each other" can't mean that every circle is in touch with each of the remaining ones as is the case with the original 3 Malfatti circles. While the original three Malfatti circles could be found solely by analytic methods (in my sheet I didn't as Mathcads symbolic would not be able to solve the necessary equations), the solution for the six circles needs to make heavily use of numerical methods. In case you have too much spare time (😉), here is the link: https://www.sciencedirect.com/science/article/pii/S0925772112000259
Good luck!!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I solved with students the problem of how a triangle fits into a circle using numerical methods - see animation above. The idea came to inscribe two, three, etc. circles in a triangle. The problem was quickly solved numerically (see pictures bellow and Prime 6 sheet in attach). Then we began to search the Internet for this topic. It turned out that our solution is much simpler and more beautiful than the existing solutions.
Compare, pls, with this for example https://mathworld.wolfram.com/MalfattiCircles.html .
Conclusion: first try to solve the problem yourself, and then check if there are already ready-made solutions.
Many decisions were made at a time when there were no means of numerical problem solving.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Nice approach, but personally I'd prefer an exact analytical (and preferably symbolic) solution over one found by numerical methods - I would consider a symbolical solution more "beautiful" even if it takes up more space and looks ugly at first sight. After all it would quickly give you a simple numerical result as soon as you feed it with numbers 😉
Unfortunately Mathcads symbolic was not powerful enough to give a symbolic solution starting with the very nicely derived equations of Wolfram Alpha.
And of course I also tried to solve your system of nine equations symbolically, but as expected there was no solution found.
The solutions you can find on the net either strive for a constructive, geometrical solution (I would not have been able to come up with any of those solutions I have seen) or an "exact" symbolical one. It looks like you have to accept some tricky detours to arrive at a general solution.
But symbolic calculations always have their narrow limits - just think of real world (systems of) differential equations - just few can be solved exactly.
And as already written above, I think that in generalizing to six circles, numerical methods are probably indispensable.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My day ended very well today - Werner said "nice approach" + a kudo from Wermer😀
Yes, hybride methods (symbolic+numeric) are the best way to problems solution/
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
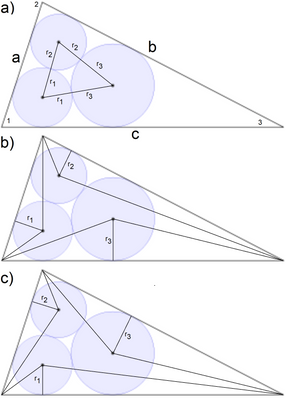
One billiards Malfatti: 12 equations with 12 unknowns - see attach!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Congratulate me! An article was published in the journal "Mathematical Education" on this discussion of ours.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@ValeryOchkov wrote:
Congratulate me! An article was published in the journal "Mathematical Education" on this discussion of ours.