Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Mathcad Precision problem
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Mathcad Precision problem
I have stumbled upon what seems to be a serious precision error with Mcad. As shown in the attached worksheet, I implemneted a function to calculate the stirling number of the second kind (S2). The stirling number of the second kind is the number of ways to partition a set of n objects into k non-empty subsets. When n=k the answer should be 1; so S2(10,10) = 1 and S2(100,100)=1. However, I found that I only get correct results for small values up to n = 25. Above that I get all kinds of errors. See the attached worksheet.
- Labels:
-
Other
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thats really bad looking and I like the way you investigated to trap the problem.
But numerical evaluations are afflicted with numerical inaccuracies by nature - while I wouldn't have believed it to be that bad, so I can understand you call it an error/bug, but probably it isn't.
Anyway - you get the correct results if you use the symbolic evaluation:
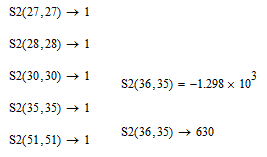
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks for the reply.
Yes, the symbolic evaluation can be used to get the correct answers; However, because of the limitations associated with the symbolic processor, it's not of much use for the problem I'm working on which requires manipulating and ploting 2D functions that have the sterling function incorporated within it.
It would be nice if Mathcad had an option that would increase the internal precision for numerical evaluations.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Look at the attached. This modified function S2 will not behave exactly like a normal numeric function in all situations, but maybe you can benefit from it nonetheless.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Your file has extension .xmcdz which doesn't open with Mathcad 14. Can you post it as .xmcd or as a PDF file.
Thanks in advance.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hmm, there is no difference in file format between MC14 and MC15 AFAIK and MC14 should be able to open xmcdz-files.
Anyway, here it is in xmcd and MC11 mcd format.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
In (my) MathCad 11.2 the definition of S2() fails with an error message of: 'This variable of function is not defined above.'
It appears it cannot evaluate the combin() function symbolically, only numerically.
"combin(3,1)=3"
"combin(3,1)->" produces an 'Unknown error.'
S2_detail() fails to produce the table, it lacks a statement to return A.
When I add a 'return A' to that function, it produces a table, and then the expression following "producing the error" results in '1' (which IS equal to the required 1!, isn't it?). No sorry, it returns 0.999868247598799; is that close enough?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
"combin(3,1)->" produces an 'Unknown error.'
You may try using numbcomb(3,1) instead or replace by the definition using factorials.
The problem with S2(), with its symbolic eval definition and problematic numeric representation reminds me of this thread: http://communities.ptc.com/message/197737#197737
Also the big differences between MC11 and newer versions seem to be covered there.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
For a while there I thought you found what I am looking for. Using the symbolic processor does give accurate results now -thanks! But it can only be used as a scalar. What's strange is that when I'm calling the function now to setup an array, you see it doing all the calculations "live" in front of your eyes! ... but they are not saved in the array!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Adnan Mustafa wrote:
For a while there I thought you found what I am looking for. Using the symbolic processor does give accurate results now -thanks! But it can only be used as a scalar. What's strange is that when I'm calling the function now to setup an array, you see it doing all the calculations "live" in front of your eyes! ... but they are not saved in the array!
Add a numeric evaluation = after the call of SS2(p,j) and it works. This seems to make the values "numeric/scalar". Unfortunately I know of no way to do that conversion aleady inside the functun S2.
But as already said, that kind of function will behave somewhat strange in some situations, as the results are not seen as scalars by Mathcad but as an expression. Thats the reason the function S2 could not be used to plot. But (depending on what plots you are after) storing the values to be plotted in vectors and then plotting them should work.
BTW, I'm not sure why, but the if-condition to catch if p<m seems to be unnecessary. The sum will yield 0 in that case anyway.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Her are a few ideas to force the symbolic processsor to produce (hopefully) "correct" answers.
Regards
Andy
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The problem with your functions ist the same as with mine http://communities.ptc.com/message/203150#203150
that the results look like scalars but aren't, they are expressions. So they will not plot, which is what Adnan Mustafa demanded.
To make your initial definition of S2(p,m) work like you expected, you can do as I did, leaving the original if-condition intact, or you simply need to set the RHS in parantheses (first insert the parentheses, then copy the symbolic eval inside).
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I've written a program that calculates n! to whatever precision you need up to 400!
The attached program outlines the method that can be expanded to even larger factorials.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Interesting approach - didn't you post a similiar sheet for calculation of pi a while ago?
How would you apply that method here to construct a function S2 with enough precision which is numerically useable also for plotting (mine isn't) as the poster demanded?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Yes, it borrows multiplication from the pi calculation.
That worksheet has addition, subtraction, multiplication, and division methods for very large numbers.
I can re-post it here or someone can look it up. It may be useful for this problem.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The question rather was how to use those functions to implement a numerically ordinary function S2() using those routines. We need an ordinary number in an ordinary variable at the end.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
What you have is really impressive, but does not help me in my problem.





