ACCEPTED SOLUTION
Accepted Solutions
Alejandro Jaramillo wrote:
Thank you for your answers, I forgot to explanied that the error apears when I define de vector "dist" for monte carlo function in MATHCAD PRIME 3.1, it says that the vector only can have the name of the distribution function, so I can´t use "rbeta(...)" or anything with arguments.
Ah. I see what you mean. I'm not sure why montecarlo is written the way it is; I would have thought, at first glance, that it would be more useful to allow the user to specify the inverse cumulative function plus necessary arguments.
You get the error you see because you can only use a function of the form F(n), where F(n) is a function that generates n samples from the distribution described by F's underlying distribution functions. The given montecarlo distribution functions, eg Normal, are implementations of their equivalent 'r' functions, eg, Normal(n) is rnorm(n,0,1) and Uniform(n) is runif(n,-6,6).
The Rvals merely scale the variants according to x = mean + stdev * x1, where x1 is a variant generated by the distribution function (eg, Normal or Uniform). This means that if the distribution function has shape parameters, then the 'dist' function must be tailored for those parameters. For example, if you want to use a beta or triangular distribution, you'll have to choose the shape you want (ie, s1 & s2 for beta, and a, b & c for triangular), then write a specific Beta(n) or Triang(n) for these parameters. Eg:
Beta(n):=rbeta(n,s1,s2)
Triang(n):=rtriang(n,a,b,c) [where rtriang is as defined in my example above]
I tried these with montecarlo, using Rvals of mean=0,stdev=1 to give unity scaling, but get a different error: "The function did not evaluate to a real value. It may include a complex value.". I even tried Uniform(n):=runif(n,-6,6), as per the Help page definition, and that gave the same error.
However, ever cloud has a silver lining, and it's not that difficult to write a version of montecarlo that will take the same input arguments and return similar results. It doesn't allow arbitrarily long distribution arrays, but, by using an if..elseif..else structure, it's possible to make this new variant handle up to 5 or so distributions. This is only possible because Prime has dropped the static typing introduced in Mathcad 12 and reverted to Mathcad 11's dynamic typing. Mathcad 12..15 would raise a function type error, because static typing would have to know beforehand (ie, as soon as you've written it not executed it) how many arguments the target function F has.
Stuart
You can find Beta distribution and many others in "Insert Function" command (in main menu select "Insert" --> "Function" --> "Probability Distribution"):
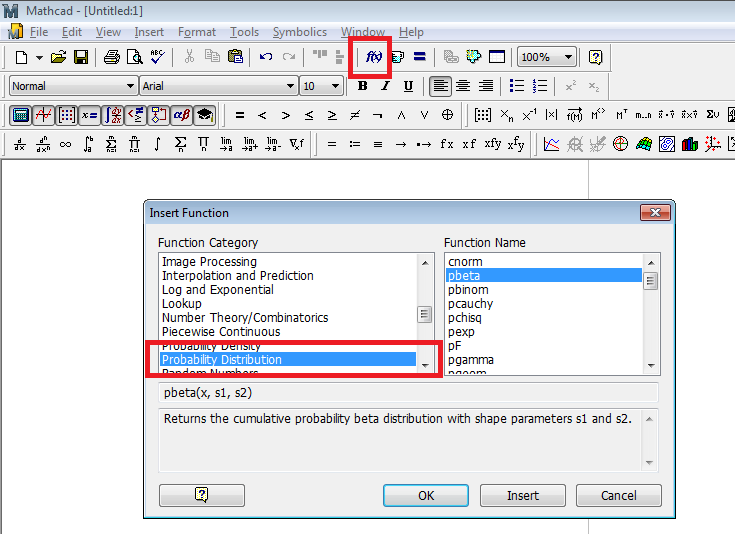
In attachment you can find an example of working with a Triangular distribution.
Alejandro Jaramillo wrote:
I know Mathcad has Normal, LogNormal, Weibull and Uniform, but I need to include a Triangular and a Beta distribution.
Here's another variant of the triangular distribution to complemet Vladimir's example. It provides density, cumulative, inverse cumulative and vector functions for the triangular distribution in keeping with Mathcad's other distribution functions.
Stuart
Alejandro Jaramillo wrote:
Thank you for your answers, I forgot to explanied that the error apears when I define de vector "dist" for monte carlo function in MATHCAD PRIME 3.1, it says that the vector only can have the name of the distribution function, so I can´t use "rbeta(...)" or anything with arguments.
Ah. I see what you mean. I'm not sure why montecarlo is written the way it is; I would have thought, at first glance, that it would be more useful to allow the user to specify the inverse cumulative function plus necessary arguments.
You get the error you see because you can only use a function of the form F(n), where F(n) is a function that generates n samples from the distribution described by F's underlying distribution functions. The given montecarlo distribution functions, eg Normal, are implementations of their equivalent 'r' functions, eg, Normal(n) is rnorm(n,0,1) and Uniform(n) is runif(n,-6,6).
The Rvals merely scale the variants according to x = mean + stdev * x1, where x1 is a variant generated by the distribution function (eg, Normal or Uniform). This means that if the distribution function has shape parameters, then the 'dist' function must be tailored for those parameters. For example, if you want to use a beta or triangular distribution, you'll have to choose the shape you want (ie, s1 & s2 for beta, and a, b & c for triangular), then write a specific Beta(n) or Triang(n) for these parameters. Eg:
Beta(n):=rbeta(n,s1,s2)
Triang(n):=rtriang(n,a,b,c) [where rtriang is as defined in my example above]
I tried these with montecarlo, using Rvals of mean=0,stdev=1 to give unity scaling, but get a different error: "The function did not evaluate to a real value. It may include a complex value.". I even tried Uniform(n):=runif(n,-6,6), as per the Help page definition, and that gave the same error.
However, ever cloud has a silver lining, and it's not that difficult to write a version of montecarlo that will take the same input arguments and return similar results. It doesn't allow arbitrarily long distribution arrays, but, by using an if..elseif..else structure, it's possible to make this new variant handle up to 5 or so distributions. This is only possible because Prime has dropped the static typing introduced in Mathcad 12 and reverted to Mathcad 11's dynamic typing. Mathcad 12..15 would raise a function type error, because static typing would have to know beforehand (ie, as soon as you've written it not executed it) how many arguments the target function F has.
Stuart
