Community Tip - Did you know you can set a signature that will be added to all your posts? Set it here! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Multiple integrals not calculating
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Multiple integrals not calculating
Hi all,
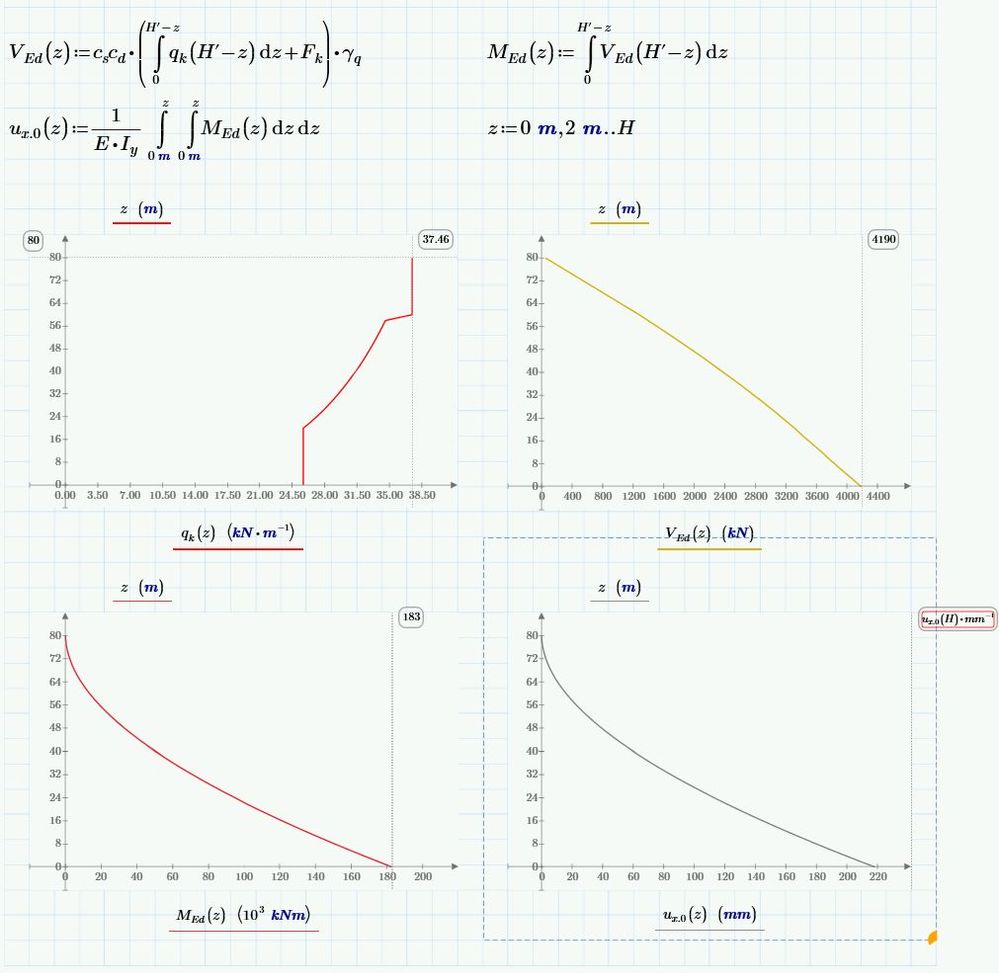
I'm working on on a sheet which calculates section forces and deflections in a cantilever beam based on a function for the load. There's multiple integrals involved:
- define q(z)
- V(z) = integrate q(z) over z = 0...z
- M(z) = integrate V(z)
- u(z) = double integration of M(z)
In my sheet this sort of looks as follows, where q is a ranged function, see the top left graph:
Steps 2 and 3 are easy for MathCAD to compute, but step 4 (bottom right graph) puts my computer in an endless loop of calculation. MathCAD 15 also has it hard, but does come to a result after a while, where MathCAD Prime 4 is still calculating after about an hour.
I can understand that multiple integrations can be cumbersome for my computer, but in my opinion, this is what MathCAD should be good at? Am I doing something wrong somewhere, are there ways to get the last step working, or am I just asking too much of the software?
Thanks in advance for your advice!
Solved! Go to Solution.
- Labels:
-
Civil_Engineering
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It takes forever? Yeah, been there!
Realize that when you integrate using a function that itself is an integral you're doing the first integration again for each step of the second. And you're four levels deep.
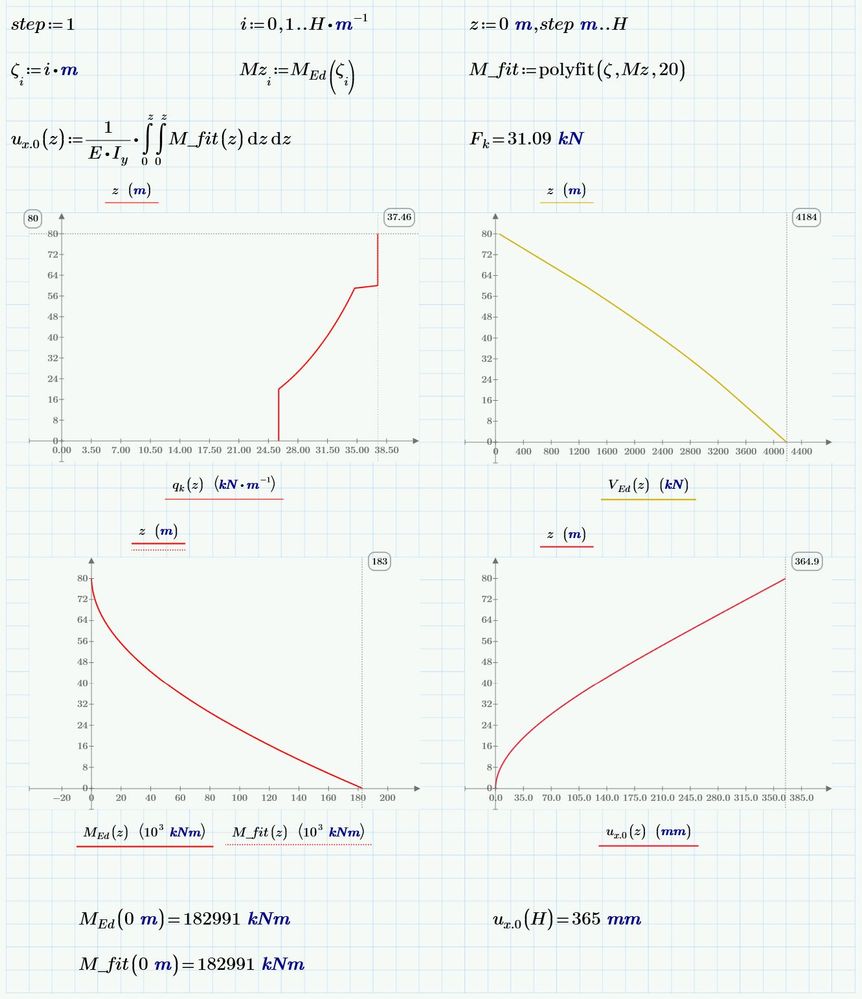
What I have found that loses accuracy if you're not really careful but speeds the process is to fit a polynomial. (Polynomials integrate very fast!) Looking at your graphs, moment looks like a good candidate.
Develop a vector (Z) along the length. Create a second vector of moments at each location of Z, (Mz), by evaluating your function. (Mz = MEd(Z)). Then use Fn:=polyfit(Z, Mz,n) to fit an nth order polynomial to that data. ( Polyfit creates a function.) You can plot the error Mz-Fn(Z),and adjust n to control errors.
Now, instead of integrating M(z), integrate Fn(z)--should be much faster.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Upload your worksheets (M15 as well as Prime 4).
Alan
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I agree fully with Alan: Upload your worksheet(s), do not post just a picture.
Other thatn that: It's usually NOT a good idea to have the very same variable in the integrand as on the borders of integration.Suggestion: change the 'z's of integrands to e.g. zeta's, that should solve most of your problem. In the double integral you are going to need zeta1 and zeta2 then.
And finally, if your Qk function is sufficiently simple, solve the whole problem purely symbolically first, ideally resulting in a closed expression for each of your functions. That will make calculations faster in the end.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My apologies, here's the sheets...
I'll give the suggestion of the integrand borders a try!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Solve it symbolically first, or do as Fred suggests: fit simpler functions to your integration results.
Some remarks (just looked at the alg-... "not include" file, because none of the files fully function in Prime express due to usage of include files and programming) :
- In your definition of q'p(z) you have a last line with an IF but no corresponding ELSE. Does that leave room for unaccounted-for situations?
- Below "achtergrondresponsefactor" (typisch Nederlands, om alles aan elkaar te schrijven) you define a function L(z) that in the ELSE part calls itself. That doesn't speed things up... Why not just return the 'THEN' expression with z replaced by zmin?
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks, of course I will check out your suggestions for improvement of the included sheet as well! (as for the language comment: Dutchies will be Dutch right? ![]() )
)
Didn't get the part with the integrand borders working though, but that's probably my basic lack of understanding math ![]()
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It takes forever? Yeah, been there!
Realize that when you integrate using a function that itself is an integral you're doing the first integration again for each step of the second. And you're four levels deep.
What I have found that loses accuracy if you're not really careful but speeds the process is to fit a polynomial. (Polynomials integrate very fast!) Looking at your graphs, moment looks like a good candidate.
Develop a vector (Z) along the length. Create a second vector of moments at each location of Z, (Mz), by evaluating your function. (Mz = MEd(Z)). Then use Fn:=polyfit(Z, Mz,n) to fit an nth order polynomial to that data. ( Polyfit creates a function.) You can plot the error Mz-Fn(Z),and adjust n to control errors.
Now, instead of integrating M(z), integrate Fn(z)--should be much faster.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thanks Fred, that seems to do the trick indeed!
Haven't been able to fully verify the results, but the calculation time is more than acceptable, considering what's being calculated!