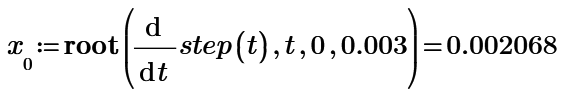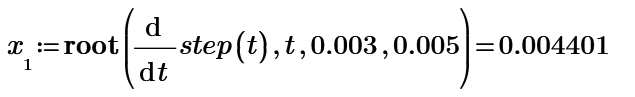Community Tip - When posting, your subject should be specific and summarize your question. Here are some additional tips on asking a great question. X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Multiple solutions for equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Multiple solutions for equation
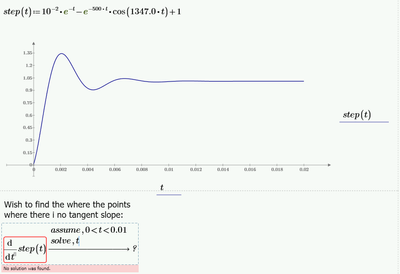
I am having troubles getting multiple solutions for this system (with an underdamped response).
I am using PTC MathCad Prime 5.0
Does anyone have suggestions?
It works to use the root function, within a specific interval, but this function does not return all the solutions. I would like an way to get the solutions without necessarily knowing the interval.
Solved! Go to Solution.
- Labels:
-
Electrical_Engineering
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thats a very old problem with the symbolic (at least since Maple was replaced by muPad).
There is no exact analytical solution for the equation you want to solve and so the symbolic switches to some kind of numeric solver and returns only one numeric result. And in this mode the symbolic unfortunately ignores modifiers like "assume" or "fully".
I guess your only chance is to use numeric methods like a solve block or the "root" function. The drawback of this is that you won't get all solution, but only one, depending on the guess value or the range you provide.
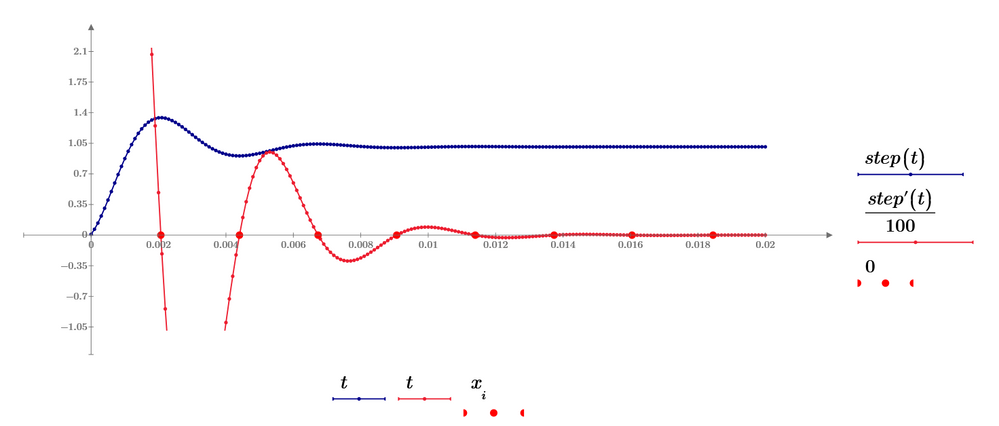
You can turn all those numeric methods into function and may call those function vectorized to get a couple of solutions.
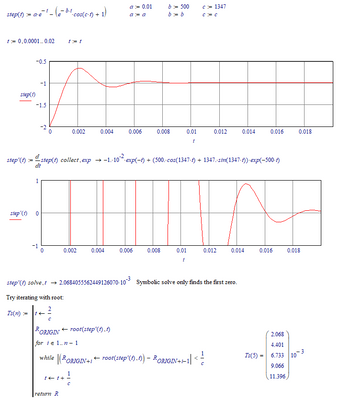
Using the root function with a guess value has the drawback, that you don't necessarily get a solution near the guess as you can see in the picture below with the guess 0.003.
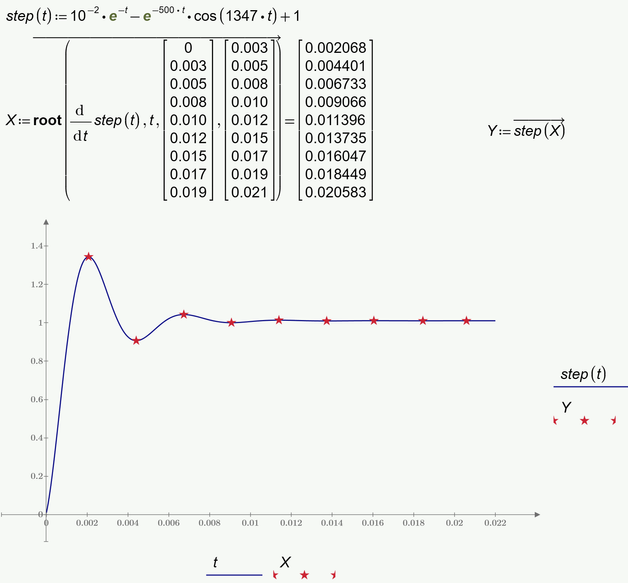
So probably in your case its more appropriate to use the "root" function by providing a range:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Try 'solve,t,all' instead of simple 'solve,t'.
Success!
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for the response. I tried it, but with the same problem as before
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This should do it:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Tags:
- Prime_7.0
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thats a very old problem with the symbolic (at least since Maple was replaced by muPad).
There is no exact analytical solution for the equation you want to solve and so the symbolic switches to some kind of numeric solver and returns only one numeric result. And in this mode the symbolic unfortunately ignores modifiers like "assume" or "fully".
I guess your only chance is to use numeric methods like a solve block or the "root" function. The drawback of this is that you won't get all solution, but only one, depending on the guess value or the range you provide.
You can turn all those numeric methods into function and may call those function vectorized to get a couple of solutions.
Using the root function with a guess value has the drawback, that you don't necessarily get a solution near the guess as you can see in the picture below with the guess 0.003.
So probably in your case its more appropriate to use the "root" function by providing a range: