- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
Multiplying range variables doesn't work
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Multiplying range variables doesn't work
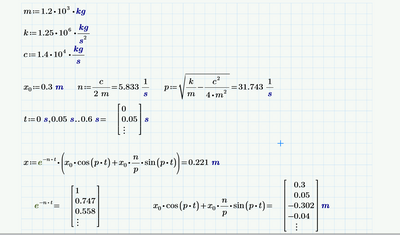
x should have more values depending on t. Why do I only get 1 value?
If I separate the terms they work as they should
Solved! Go to Solution.
- Labels:
-
Mathcad Usage
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First let me say that whenever possible you should always attach the worksheet itself.
You defined a range t and in the same region you numerically evaluated it (the = sign after the definition). This is an undocumented trick to turn a range into a vector.
So t is a vector.
x is defined as a product of two factors and as you show yourself in the last line, both factors are vectors. And the "normal" product of two vectors is ... one single scalar (dot product, scalar product).
To get the result you expect, you must vectorize (the arrow operator over an expression) the right hand side of the definition of x.
Keep in mind that e^t actually should throw an error because there is no definition in math to take a number to the power of a vector. Prime instead applies automatic implicit vectorization in that case (also applies to sin(t), etc) and evaluates that expression for each vector el/ement in a row and collects the various results in its result vector - excactly what you had in mind. Multiplication on the other hand is an operation defined for vectors and if you want it to be executed elementwise again, you must manually vectorize the operation.#
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
First let me say that whenever possible you should always attach the worksheet itself.
You defined a range t and in the same region you numerically evaluated it (the = sign after the definition). This is an undocumented trick to turn a range into a vector.
So t is a vector.
x is defined as a product of two factors and as you show yourself in the last line, both factors are vectors. And the "normal" product of two vectors is ... one single scalar (dot product, scalar product).
To get the result you expect, you must vectorize (the arrow operator over an expression) the right hand side of the definition of x.
Keep in mind that e^t actually should throw an error because there is no definition in math to take a number to the power of a vector. Prime instead applies automatic implicit vectorization in that case (also applies to sin(t), etc) and evaluates that expression for each vector el/ement in a row and collects the various results in its result vector - excactly what you had in mind. Multiplication on the other hand is an operation defined for vectors and if you want it to be executed elementwise again, you must manually vectorize the operation.#
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you for your answer! After some trial and error with easy examples I realised that multiplying 2 vectors results in multiplying both elements from the respectiv row and adding them up. The way I managed to fix this is by turning it into a function.
In case it might help someone
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@TS_9501702 wrote:
Thank you for your answer! After some trial and error with easy examples I realised that multiplying 2 vectors results in multiplying both elements from the respectiv row and adding them up.
Yes, thats exactly what vector dot product (inner product, scalar product) means 😉
And if you apply vectorization, you get the result you expected. See her for comparison:
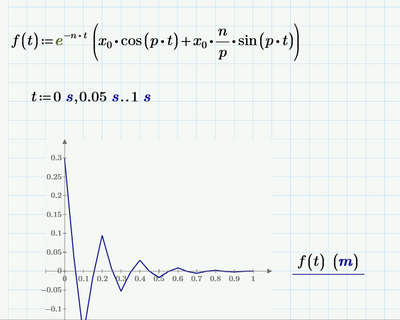
But turning the calculation into a function as you finally did usually is the better approach anyway. You need the t-range just for plotting and you sure should choose a smaller step-width: