Community Tip - You can Bookmark boards, posts or articles that you'd like to access again easily! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
My question:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
My question:
Imagine a plain (x,y) with 3 points (x1,y1), (x2,y2), (x3,y3) at it, not positioned in a line.
At each of the 3 points is fixed a straight wire with given length L1, L2, L3, protruding to z-space.
Find the spatial coordinates of the point (x,y,z), where the 3 ends of the wires can find together.
From Wolfgang Issel using MC14 on Windows 7
Solved! Go to Solution.
- Labels:
-
Other
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems to me that WOLFGANG ISSEL is asking how to find intersection point of three spheres.
MH
Martin Hanák
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
This problem is not sufficiently defined.
Given any point not on the plane you can connect a straight line to the three points, (Two points define a straight line.) If the lines are normal to the plane (protruding into z-space) then they will never intersect.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems to me that WOLFGANG ISSEL is asking how to find intersection point of three spheres.
MH
Martin Hanák
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
If the lengths of the "wires" are specified then you are correct--this is the intersection point of three spheres.
Which then changes into problems for which there are n solutions, where n can be 0, 1 or ??
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
...2 solutions:

One example with (essentially) a single solution:
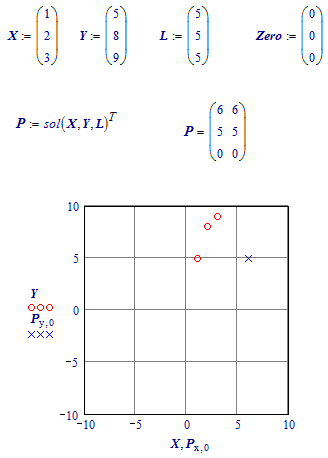
The red dots are the locations of the three points on the z=0 plane.
The blue cross is the projection of P on the z=0 plane.
Two solutions:

Note that two solutions for P are found, symmetrically w.r.t. the z=0 plane.
And of course there's the no (real) solution:

With the restriction that the three points on the z=0 plane are not on a single line, the case where you would infinite solutions (if the three points are the same, and the three lengths are the same) does not exist.
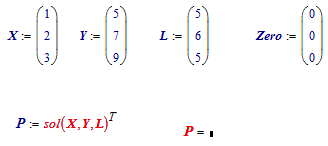
"Found a singularity".
and:
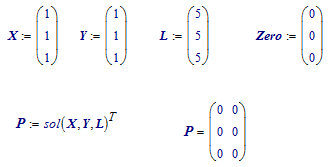
Ah, tricked by Maple providing only the Zero solution.
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Luc,
thank You for Your solution. Compared with the solution from F.M. and Fred K. the same results were obtained.
To be sure I verified these with a real model and also found accordance.
So my problem is solved in a very fast and elegant way.
Greetings from Wolfgang Issel
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello Fred,
thank You for Your solution. I compared it with the solution from F.M. and got the same results. To be sure I verified these with a real model and also found accordance.
So my problem is solved in a fast and elegant way.
Greetings from Wolfgang Issel
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
It seems to me, insted, that hi is looking for the coordinates of the point P represented in the figure, knowing the coordinates of the three points P1, P2, P3 lying on the plane z = 0, and the lengths L1, L2 and L3: :

in other words:
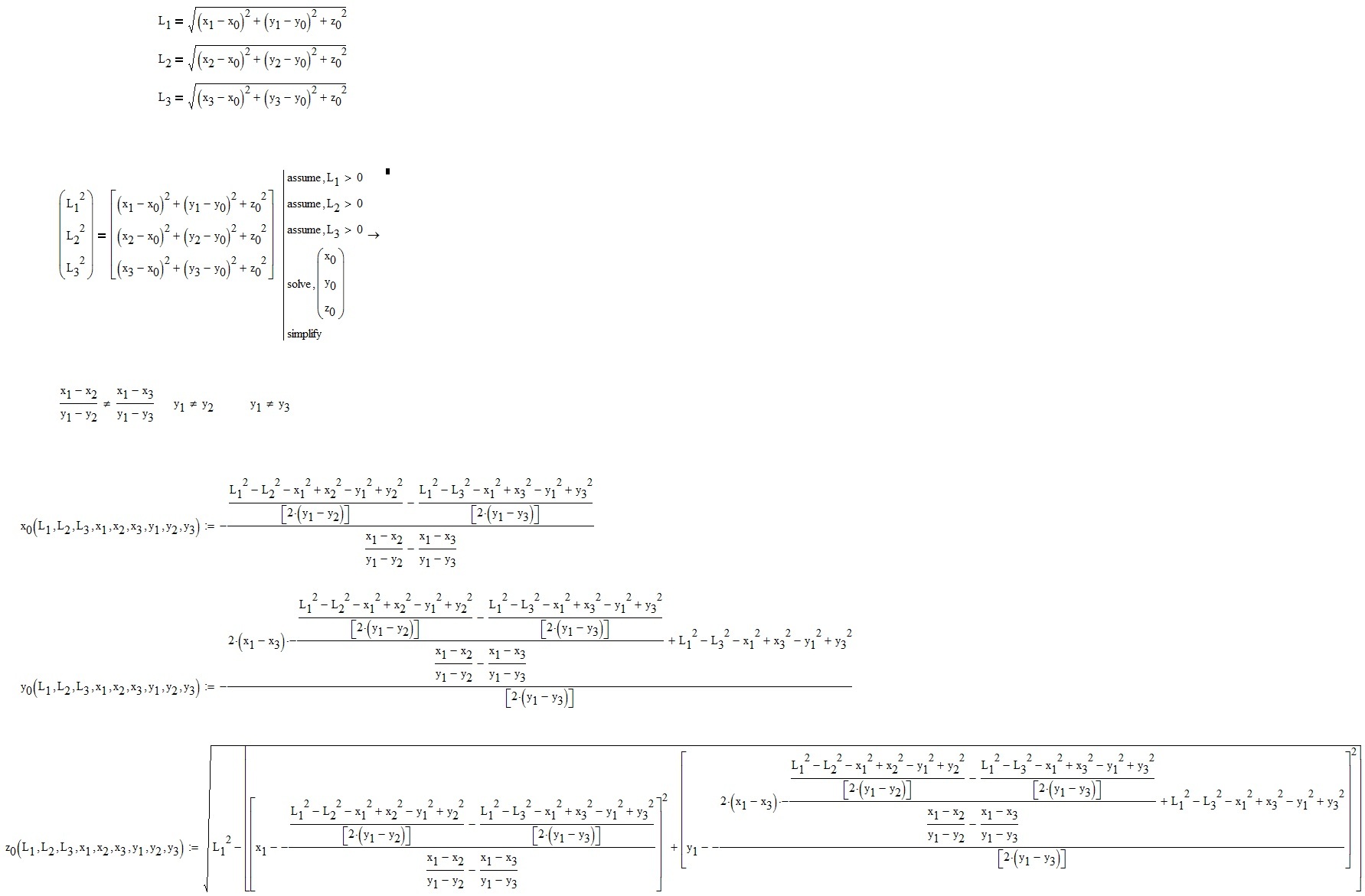
of course you have to avoid the imaginary solutions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hello F.M.,
thank You for Your solution and Your MC-Sheet. I compared it with the solution of Fred Kohlhepp and got the same results. I also found accordance when I verified these with a real model (straight wires with given length starting at there respectively coordinates).
So my problem is solved in a fast and elegant way and I can continue my work.
Greetings from Wolfgang Issel





