New problem with a catenary – a specific pendulum

[ValeryOchkov]

New problem of the catenary – a specific pendulum.

We loaded our catenary with weight and looked like changing its form – see please here http://communities.ptc.com/videos/4438. If the weight is too heavy, then either Mathcad not be able to solve a system of equations or a catenary... breaks and we have two parts as a… pendulum. I tried to simulate the swing of this pendulum-chain with five units - see please http://communities.ptc.com/videos/4448

The problem we have is not a chain, and a weighty chain is flexible, which we rejected from the vertical to the desired form (with what desired form?). And released. How to simulate the swing of this pendulum-chain? Is there a symbolic solution of this problem. There is solution is for the ordinary pendulum.

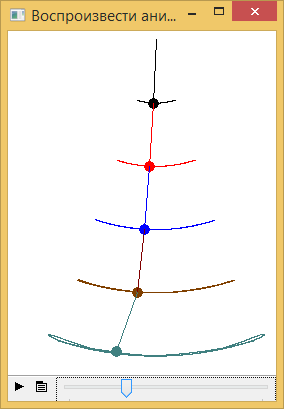
ЗЫ

"Knowledge will break the chains of slavery"

[ValeryOchkov]

An animation for 10 ball - see the attach too!

What is the best initial position of balls? The catanery line?

Can we create a sheet with infinity number of balls?

Etc...

Video Link : 4509

[Fred_Kohlhepp]

Your 10 mass pendulum has (if my accounting is right) 55 different degrees of freedom; the motion solution has multiple answers that will depend on the initial displacement arrangements.

[ValeryOchkov]

Thanks, Fred.

The problem is very interesting. I can not find something about it in Internet

One real video:

Video Link : 4511

[ValeryOchkov]

Fred Kohlhepp wrote:

Your 10 mass pendulum has (if my accounting is right) 55 different degrees of freedom; the motion solution has multiple answers that will depend on the initial displacement arrangements.

One initial displacement arrangements:

[Fred_Kohlhepp]

There's a large amount of analysis for compound pendulums; your problem has the additional complication of flexible links but that might be a place to start. (A Lagrangian analysis seems to be a favorite starting place.

[ValeryOchkov]

Thanks Fred.

One general question.

There is a mathematic pendulum see for example here

Can we say about a mathematic pendulum-catenary? About its period etc.

PS

A mathematic (a=sin a) and physical Pendulum solutions in Maple:

[ValeryOchkov]

Fred Kohlhepp wrote:

Your 10 mass pendulum has (if my accounting is right) 55 different degrees of freedom

Does my catanery-pendulum have an infinity degrees of freedom?

I feel this problem has a simple solution by specisic initial position of athe catenary.

[Fred_Kohlhepp]

Combine a pendulum with a vibrating string.

[ValeryOchkov]

Fred Kohlhepp wrote:

Combine a pendulum with a vibrating string.

Like this http://communities.ptc.com/videos/1357 ?

[ValeryOchkov]

Daniel Bernoulli has solved this problem in 1732 (in Russia ?) - see http://librarum.org/book/5372/689

But now we can try to solve it numerical without constrains. In Mathcad. With animation.

[ValeryOchkov]

One fine pendulum lesson in the Amarcord by Federico Fellini!

The teacher has a catenery (chain) on his stomach for new demonstration

[Fred_Kohlhepp]

Actually, as demonstrated by the segment of cord between the professor's hands, this is a catenary. The relative mass of the "chain" to the weight is such that it's not visually obvious, but the "pendulum arm" is flexible.

[ValeryOchkov]

Fred Kohlhepp wrote:

Actually, as demonstrated by the segment of cord between the professor's hands, this is a catenary.

Ops - one more catenary - Thanks Fred!

[ValeryOchkov]

One solution in Maple

http://vuz.exponenta.ru/PDF/SOL/cep.html