Non-Trivial Symbolic Solutions

[Anousheh]

Hello,

Please help me to solve symbolically:

y"+4y=0 (non-trivial solution)

Thank you so much for the time and help.

[MikeArmstrong]

Solve for what?

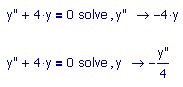
Mike

[Anousheh]

Thank you Mike,

The condition y(0)=1 should be satisfied.

The correct answer should be y=Cos(2x)

Please help if you can

Thanks

[AWesterman-disa]

Hi Anousheh

I don't know if the symbolic engine can handle this type of question as the result is somewhat indeterminate

From the Odesolve part of the attached file you can obtain a numerical solution which shows some form of trigonometric function.

Varying the initial conditions y'(t0)=y'0 and y(t1)=y1 in the odesolve block will give solutions including sin(t), cos(t) and many other variations.

The symbolic calculations following also show the possibilities but there will be many more possible valid solutions.

[Anousheh]

Thank you A Westerman,

I have the condition y(0)=1 that should be satisfied.

The correct answer is y=Cos(2x)

Please help

Thank you

[ValeryOchkov]

Anousheh Rouzbehani wrote:

Thank you A Westerman,

I have the condition y(0)=1 that should be satisfied.

The correct answer is y=Cos(2x)

Please help

Thank you

Sorry, but must be two conditions - the ODE has a 2-d order.

[Anousheh]

OK

Let's say the second condition is: y'(0)=0.5

Thanks

[Anousheh]

Hello A Westerman,

Thanks again for your valuable information.

Please see the following ODE:

y'=F(x,y) [y prime]

with the prescribed initial condition y(x0)=y0

How do we solve this kind of ODE?

Thanks so much.

Anousheh

[AWesterman-disa]

Hi Anousheh,

difficult to know exactly what you need. Can you post an example of the function(s) you are interested in - (save as ver 12 or lower as I only have access to ver 12).

The quicksheets tend to be a good starting resource & may give you an insight into what is possible.

one option from them attached as a simple example.

regards

Andy

[ValeryOchkov]

Anousheh Rouzbehani wrote:

Hello,

Please help me to solve symbolically:

y"+4y=0 (non-trivial solution)

Thank you so much for the time and help.

C1*sin(2x)+C2*cos(2x)

Sorry,

what is it "non-trivial solution"?

[Anousheh]

Thank you so much.

The correct answer should be y=Cos(2x), this satisfies the condition y(0)=1

Can you help please?

[ValeryOchkov]

Anousheh Rouzbehani wrote:

Thank you so much.

The correct answer should be y=Cos(2x), this satisfies the condition y(0)=1

Can you help please?

Sorry, but what help do you need?