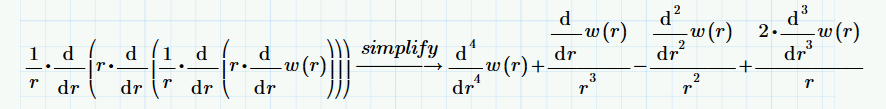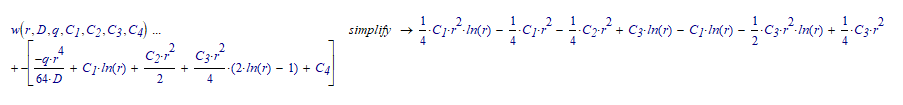Community Tip - Need to share some code when posting a question or reply? Make sure to use the "Insert code sample" menu option. Learn more! X
- Subscribe to RSS Feed
- Mark Topic as New
- Mark Topic as Read
- Float this Topic for Current User
- Bookmark
- Subscribe
- Mute
- Printer Friendly Page
ODE Illegal context
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
ODE Illegal context
Hello,
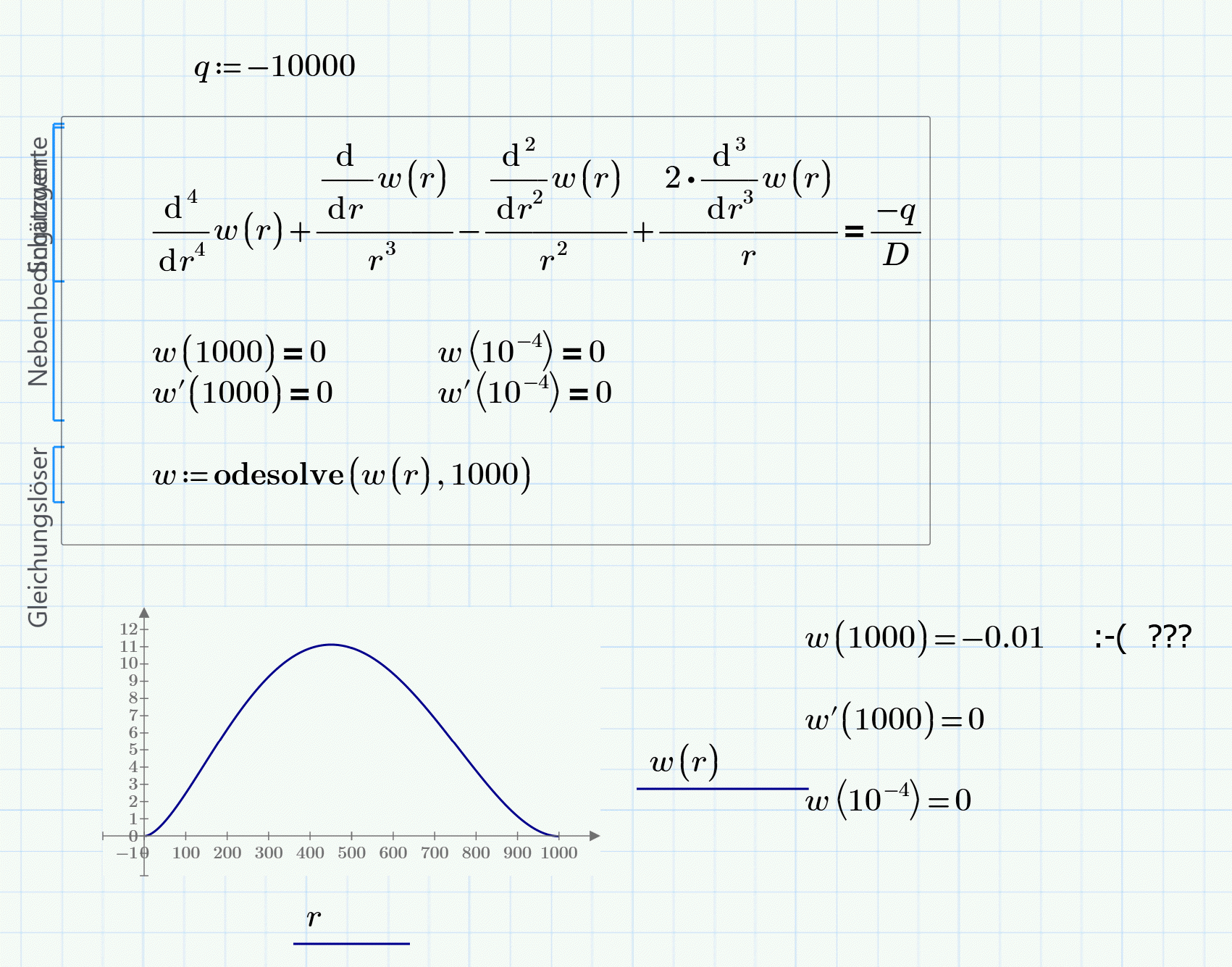
I am trying to solve a differential equation for a clamped Circular Kirchhoff-Love plate.
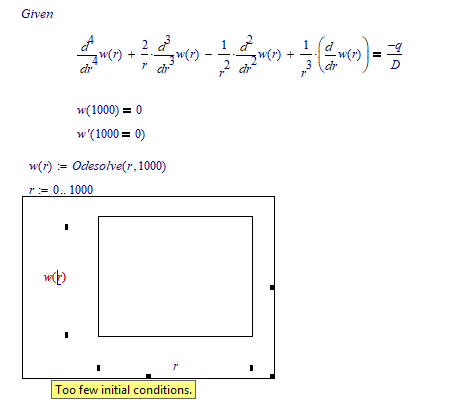
Why am I getting this error in my displacement function w(r)?
Solved! Go to Solution.
- Labels:
-
Calculus_Derivatives
Accepted Solutions
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So we can't use w(0)=0 as initial conditions as I did and you need to provide a new fourth condition.
How about w''(0)=0 ?
EDIT: I am not into mechanics myself so I am not sure but maybe Chapter 4 here
http://imechanica.org/files/4_Bending%20of%20plates.pdf
can help you to find two reasonable additional initial conditions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Attach please the Mathcad Prime sheet!
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here you are!
You have to expand the nested derivatives to make it work (best done symbolically, like Fred had shown) and you have to add two more initial conditions:
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The thing is, when r=0 -> center of the plate in cylindrical coordinates , I don't know the value, in fact, that's the value I will be looking for, because it will be the maximum deflection of the circular plate.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Probably because you're trying to solve a fourth order differential equation
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Oh, so what are the restrictions when trying to solve differential equations?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I would have expected 4 initial conditions for a fourth order DE, not just 2.
What are the values of q and D?
When Valery asked for the sheet he meant the mcdx file so we can open it in Prime. Chances are you will have to zip it first before you can upload it here because of a severe bug in the forum software.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
That will be a circular plate with a uniform loading that's clamped at the edge. So I guess we can set w'(0)=0
I was retrieving the values from a PRT file, but q and D can be whatever.
The file is attached.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
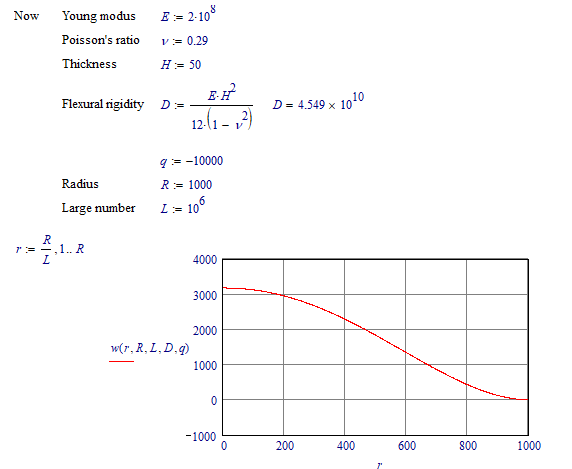
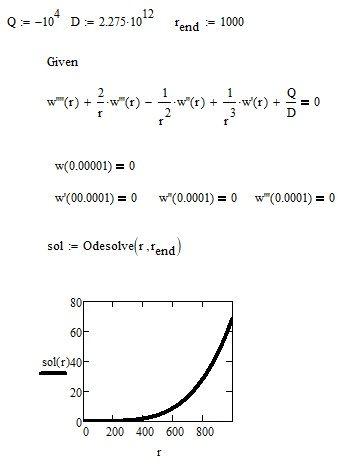
In the meantime I played around with Mathcad 15 (much faster and more capable and comfortable) and assigned arbitrary values for q and D and added two more initial conditions.
You can't use w(0) or w'(0) as your expression is not defined for r=0 (divison by zero!)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Maybe I'm missing something, either from my calculus classes or from my applied mechanics one. But can anyone here help me in getting to this (image attached) without actually utilizing the analytical solution?
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Here's the full solution for any value of q, D and R(adius of the disk):
So with that we should be able to continue as follows:
This function is large, but that does not prevent us from using it:
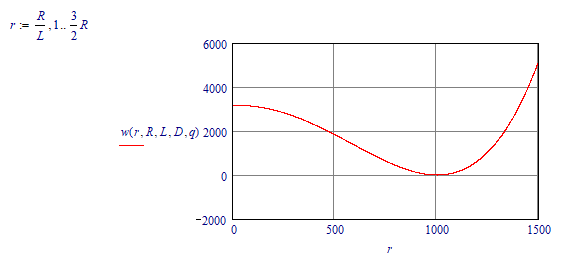
And we can even see what it does (or would do) for values of r beyond the size of the disk R:
Success!
Luc
Notice! However that my result differs from the one your picture, when I subtract them I don't get 0:
So far I wasn't able to locate where I went wrong.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
I get this:
Too few initial conditions...{also when the second is correctly written as w'(1000)=0}
You must add two (it's a fourth order).
I can't open you .prt file.... What are values for q and D ?
Luc
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Hi,
I have chosen Adams/BDF,
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
The thing is, when r=0 -> center of the plate in cylindrical coordinates , I don't know the value, in fact, that's the value I will be looking for, because it will be the maximum deflection of the circular plate.
What I know is that at the edge of the circular plate (r=1000) my deflection is 0, as well as my angle (clamped)
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
So we can't use w(0)=0 as initial conditions as I did and you need to provide a new fourth condition.
How about w''(0)=0 ?
EDIT: I am not into mechanics myself so I am not sure but maybe Chapter 4 here
http://imechanica.org/files/4_Bending%20of%20plates.pdf
can help you to find two reasonable additional initial conditions.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Thank you so much. I will be using that.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
@lferreira wrote:
Thank you so much. I will be using that.
Careful! As already said I have no mechanical background so I have no idea if setting w''(0)=0 is reasonable at all for your application.
- Mark as New
- Bookmark
- Subscribe
- Mute
- Subscribe to RSS Feed
- Permalink
- Notify Moderator
Seems to me you can define deflection and slope at the edge (zero deflection and zero slope, clamped, AKA fixed) and at the center (max deflection, tabulated equation, zero slope, it's the max deflection).
That said, I haven't been able to make it work.